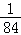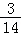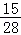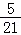2009年四川省高考数学试卷(理科)(含解析版)
2009年四川省高考数学试卷(理科)
一、选择题(共12小题,每小题5分,满分60分)
1.(5分)设集合S={x||x|<5},T={x|x2+4x﹣21<0},则S∩T=( )
A.{x|﹣7<x<﹣5}B.{x|3<x<5}
C.{x|﹣5<x<3} D.{x|﹣7<x<5}
2.(5分)已知函数 连续,则常数a的值是( )
连续,则常数a的值是( )
A.2B.3 C.4 D.5
3.(5分)复数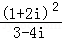 的值是( )
的值是( )
A.﹣1B.1 C.﹣i D.i
4.(5分)已知函数f(x)=﹣sin(x+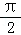 ),(x∈R),下面结论错误的是( )
),(x∈R),下面结论错误的是( )
A.函数f(x)的最小正周期为2π
B.函数f(x)在区间[0,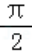 ]上是增函数
]上是增函数
C.函数f(x)的图象关于直线x=0对称
D.函数f(x)是奇函数
5.(5分)如图,已知六棱锥P﹣ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB则下列结论正确的是( )
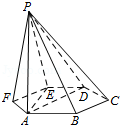
A.PB⊥AD
B.平面PAB⊥平面PBC
C.直线BC∥平面PAE
D.直线PD与平面ABC所成的角为45°
6.(5分)已知a,b,c,d为实数,且c>d.则“a>b”是“a﹣c>b﹣d”的( )
A.充分而不必要条件B.必要而不充分条件
C.充要条件D.既不充分也不必要条件
7.(5分)已知双曲线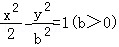 的左、右焦点分别是F1、F2,其一条渐近线方程为y=x,点
的左、右焦点分别是F1、F2,其一条渐近线方程为y=x,点 在双曲线上、则
在双曲线上、则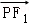 •
•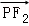 =( )
=( )
A.﹣12B.﹣2 C.0 D.4
8.(5分)如图,在半径为3的球面上有A、B、C三点,∠ABC=90°,BA=BC,球心O到平面ABC的距离是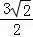 ,则B、C两点的球面距离是( )
,则B、C两点的球面距离是( )
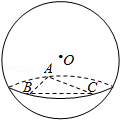
A.B.π C.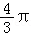 D.2π
D.2π
9.(5分)已知直线l1:4x﹣3y+6=0和直线l2:x=﹣1,抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是( )
A.B.2 C.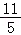 D.3
D.3
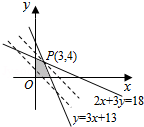
10.(5分)某企业生产甲、乙两种产品.已知生产每吨甲产品要用A原料3吨、B原料2吨;生产每吨乙产品要用A原料1吨、B原料3吨.销售每吨甲产品可获得利润5万元、每吨乙产品可获得利润3万元.该企业在一个生产周期内消耗A原料不超过13吨、B原料不超过18吨,那么该企业可获得最大利润是( )
A.12万元B.20万元 C.25万元 D.27万元
11.(5分)2位男生和3位女生共5位同学站成一排,若男生甲不站两端,3位女生中有且只有两位女生相邻,则不同排法的种数是( )
A.60B.48 C.42 D.36
12.(5分)已知函数f(x)是定义在实数集R上的不恒为零的偶函数,且对任意实数x都有xf(x+1)=(1+x)f(x),则 的值是( )
的值是( )
A.0B.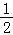 C.1 D.
C.1 D.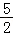
二、填空题(共4小题,每小题4分,满分16分)
13.(4分)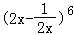 的展开式的常数项是 (用数字作答)
的展开式的常数项是 (用数字作答)
14.(4分)若⊙O1:x2+y2=5与⊙O2:(x﹣m)2+y2=20(m∈R)相交于A、B两点,且两圆在点A处的切线互相垂直,则线段AB的长度是 .
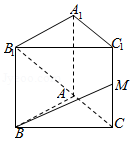
15.(4分)如图所示,已知正三棱柱ABC﹣A1B1C1的各条棱长都相等,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是 .
16.(4分)设V是已知平面M上所有向量的集合,对于映射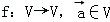 ,记
,记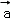 的象为
的象为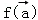 .若映射f:V→V满足:对所有
.若映射f:V→V满足:对所有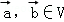 及任意实数λ,μ都有
及任意实数λ,μ都有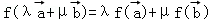 ,则f称为平面M上的线性变换.现有下列命题:
,则f称为平面M上的线性变换.现有下列命题:
①设f是平面M上的线性变换,则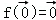
②对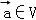 设
设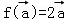 ,则f是平面M上的线性变换;
,则f是平面M上的线性变换;
③若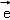 是平面M上的单位向量,对
是平面M上的单位向量,对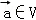 设
设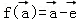 ,则f是平面M上的线性变换;
,则f是平面M上的线性变换;
④设f是平面M上的线性变换,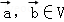 ,若
,若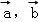 共线,则
共线,则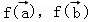 也共线.
也共线.
其中真命题是 (写出所有真命题的序号)
三、解答题(共6小题,满分74分)
17.(12分)在△ABC中,A、B为锐角,角A、B、C所对的边分别为a、b、c,且cos2A=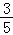 ,sinB=
,sinB=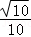 .
.
(1)求A+B的值;
(2)若a﹣b=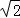 ﹣1,求a、b、c的值.
﹣1,求a、b、c的值.
18.(12分)为振兴旅游业,四川省2009年面向国内发行总量为2000万张的熊猫优惠卡,向省外人士发行的是熊猫金卡(简称金卡),向省内人士发行的是熊猫银卡(简称银卡).某旅游公司组织了一个有36名游客的旅游团到四川名胜旅游,其中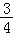 是省外游客,其余是省内游客.在省外游客中有
是省外游客,其余是省内游客.在省外游客中有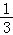 持金卡,在省内游客中有
持金卡,在省内游客中有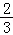 持银卡.
持银卡.
(Ⅰ)在该团中随机采访3名游客,求恰有1人持金卡且持银卡者少于2人的概率;
(Ⅱ)在该团的境内游客中随机采访3名游客,设其中持银卡人数为随机变量ξ,求ξ的分布列及数学期望Eξ.
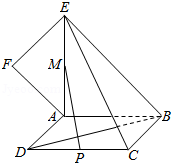
19.(12分)如图,正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直,△ABE是等腰直角三角形,AB=AE,FA=FE,∠AEF=45°
(I)求证:EF⊥平面BCE;
(Ⅱ)设线段CD、AE的中点分别为P、M,求证:PM∥平面BCE;
(Ⅲ)求二面角F﹣BD﹣A的大小.
20.(12分)已知椭圆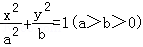 的左、右焦点分别为F1、F2,离心率
的左、右焦点分别为F1、F2,离心率 ,右准线方程为x=2.
,右准线方程为x=2.
(1)求椭圆的标准方程;
(2)过点F1的直线l与该椭圆交于M、N两点,且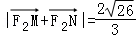 ,求直线l的方程.
,求直线l的方程.
21.(12分)已知a>0且a≠1,函数f(x)=loga(1﹣ax).
(1)求函数f(x)的定义域,并判断f(x)的单调性;
(2)若n∈N*,求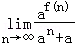 ;
;
(3)当a=e(e为自然对数的底数)时,设h(x)=(1﹣ef(x))(x2﹣m+1).若函数的极值存在,求实数m的取值范围以及函数h(x)的极值.
22.(14分)设数列{an}的前n项和为Sn,对任意的正整数n,都有an=5Sn+1成立,记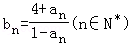 .
.
(Ⅰ)求数列{bn}的通项公式;
(Ⅱ)记cn=b2n﹣b2n﹣1(n∈N*),设数列{cn}的前n项和为Tn,求证:对任意正整数n都有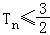 ;
;
(Ⅲ)设数列{bn}的前n项和为Rn.已知正实数λ满足:对任意正整数nRn≤λn恒成立,求λ的最小值.
2009年四川省高考数学试卷(理科)
参考答案与试题解析
一、选择题(共12小题,每小题5分,满分60分)
1.(5分)设集合S={x||x|<5},T={x|x2+4x﹣21<0},则S∩T=( )
A.{x|﹣7<x<﹣5}B.{x|3<x<5}
C.{x|﹣5<x<3} D.{x|﹣7<x<5}
【考点】1E:交集及其运算;7E:其他不等式的解法.菁优网版权所有
【分析】由绝对值的意义解出集合S,再解出集合T,求交集即可.
【解答】解:由S={x|﹣5<x<5},T={x|﹣7<x<3}故S∩T={x|﹣5<x<3},
故选:C.
【点评】本小题考查解含有绝对值的不等式、一元二次不等式,考查集合的运算,基础题.
2.(5分)已知函数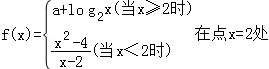 连续,则常数a的值是( )
连续,则常数a的值是( )
A.2B.3 C.4 D.5
【考点】63:导数的运算.菁优网版权所有
【专题】11:计算题.
【分析】根据x=2的左右极限和x=2时的函数值,结合函数在一点处的连续性的定义求解.
【解答】解:由题意得:
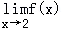 =
=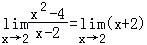 =4,
=4,
又∵f(2)=a+log22=a+1,
由函数在一点处的连续性的定义知f(2)=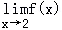 ,
,
故a+1=4,
解得a=3.
故选:B.
【点评】本小题考查分段函数的连续性,是简单的基础题.函数f(x)在点x0连续的充要条件是:函数f(x)在点x0既是右连续,又是左连续.
3.(5分)复数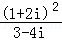 的值是( )
的值是( )
A.﹣1B.1 C.﹣i D.i
【考点】A5:复数的运算.菁优网版权所有
【专题】11:计算题.
【分析】本题是一个复数的运算,包括除法和乘方,解题时要先计算分子上的乘方,再计算除法,注意虚数单位i的运算性质.
【解答】解:∵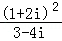 =
=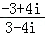
=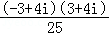
=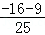 =﹣1,
=﹣1,
∴原式=﹣1
故选:A.
【点评】本题是一个复数的运算,包括除法和乘方运算,实际上是复数的除法运算,解题时只要分子和分母同乘以分母的共轭复数,就可以得到结果.
4.(5分)已知函数f(x)=﹣sin(x+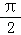 ),(x∈R),下面结论错误的是( )
),(x∈R),下面结论错误的是( )
A.函数f(x)的最小正周期为2π
B.函数f(x)在区间[0,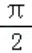 ]上是增函数
]上是增函数
C.函数f(x)的图象关于直线x=0对称
D.函数f(x)是奇函数
【考点】H9:余弦函数的定义域和值域;HB:余弦函数的对称性.菁优网版权所有
【专题】15:综合题;34:方程思想;4G:演绎法;57:三角函数的图像与性质.
【分析】由题意,f(x)=﹣cosx,可得A,B,C正确,判断D错误,可得结论.
【解答】解:由题意,f(x)=﹣cosx,可得A,B,C正确,
由于f(﹣x)=﹣cosx=f(x),函数是偶函数,即D错误,
故选:D.
【点评】本题主要考查三角函数的图象与性质,属于基础题.
5.(5分)如图,已知六棱锥P﹣ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB则下列结论正确的是( )
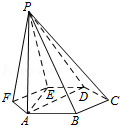
A.PB⊥AD
B.平面PAB⊥平面PBC
C.直线BC∥平面PAE
D.直线PD与平面ABC所成的角为45°
【考点】LW:直线与平面垂直;MI:直线与平面所成的角.菁优网版权所有
【分析】利用题中条件,逐一分析答案,通过排除和筛选,得到正确答案.
【解答】解:∵AD与PB在平面的射影AB不垂直,
所以A不成立,又,平面PAB⊥平面PAE,
所以平面PAB⊥平面PBC也不成立;BC∥AD∥平面PAD,
∴直线BC∥平面PAE也不成立.
在Rt△PAD中,PA=AD=2AB,∴∠PDA=45°,
故选:D.
【点评】本题考查直线与平面成的角、直线与平面垂直的性质.
6.(5分)已知a,b,c,d为实数,且c>d.则“a>b”是“a﹣c>b﹣d”的( )
A.充分而不必要条件B.必要而不充分条件
C.充要条件D.既不充分也不必要条件
【考点】29:充分条件、必要条件、充要条件;71:不等关系与不等式.菁优网版权所有
【分析】由题意看命题“a>b”与命题“a﹣c>b﹣d”是否能互推,然后根据必要条件、充分条件和充要条件的定义进行判断.
【解答】解:∵a﹣c>b﹣d,c>d两个同向不等式相加得a>b
但c>d,a>b⇒a﹣c>b﹣d.
例如a=2,b=1,c=﹣1,d=﹣3时,a﹣c<b﹣d.
故选:B.
【点评】此题主要考查必要条件、充分条件和充要条件的定义,是一道基础题.
7.(5分)已知双曲线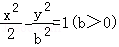 的左、右焦点分别是F1、F2,其一条渐近线方程为y=x,点
的左、右焦点分别是F1、F2,其一条渐近线方程为y=x,点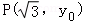 在双曲线上、则
在双曲线上、则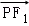 •
•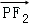 =( )
=( )
A.﹣12B.﹣2 C.0 D.4
【考点】9O:平面向量数量积的性质及其运算;KC:双曲线的性质.菁优网版权所有
【专题】11:计算题.
【分析】由双曲线的渐近线方程,不难给出a,b的关系,代入即可求出双曲线的标准方程,进而可以求出F1、F2,及P点坐标,求出向量坐标后代入向量内积公式即可求解.
【解答】解:由渐近线方程为y=x知双曲线是等轴双曲线,
∴双曲线方程是x2﹣y2=2,
于是两焦点坐标分别是F1(﹣2,0)和F2(2,0),
且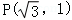 或
或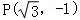 、
、
不妨令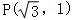 ,
,
则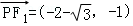 ,
,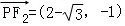
∴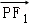 •
•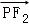 =
=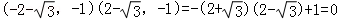
故选:C.
【点评】本题考查的知识点是双曲线的简单性质和平面向量的数量积运算,处理的关键是熟练掌握双曲线的性质(顶点、焦点、渐近线、实轴、虚轴等与 a,b,c的关系),求出满足条件的向量的坐标后,再转化为平面向量的数量积运算.
8.(5分)如图,在半径为3的球面上有A、B、C三点,∠ABC=90°,BA=BC,球心O到平面ABC的距离是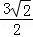 ,则B、C两点的球面距离是( )
,则B、C两点的球面距离是( )
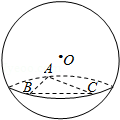
A.B.π C.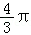 D.2π
D.2π
【考点】ND:球的性质.菁优网版权所有
【专题】11:计算题.
【分析】欲求B、C两点的球面距离,即要求出球心角∠BOC,将其置于三角形BOC中解决.
【解答】解:∵AC是小圆的直径.
所以过球心O作小圆的垂线,垂足O′是AC的中点.
O′C=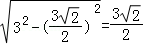 ,AC=3
,AC=3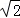 ,
,
∴BC=3,即BC=OB=OC.∴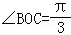 ,
,
则B、C两点的球面距离=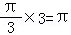 .
.
故选:B.
【点评】高考中时常出现与球有关的题目的考查,这类题目具有一定的难度.在球的问题解答时,有时若能通过构造加以转化,往往能化难为易,方便简洁.解有关球面距离的问题,最关键是突出球心,找出数量关系.
9.(5分)已知直线l1:4x﹣3y+6=0和直线l2:x=﹣1,抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是( )
A.B.2 C.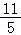 D.3
D.3
【考点】IT:点到直线的距离公式.菁优网版权所有
【专题】11:计算题.
【分析】设出抛物线上一点P的坐标,然后利用点到直线的距离公式分别求出P到直线l1和直线l2的距离d1和d2,求出d1+d2,利用二次函数求最值的方法即可求出距离之和的最小值.
【解答】解:设抛物线上的一点P的坐标为(a2,2a),则P到直线l2:x=﹣1的距离d2=a2+1;
P到直线l1:4x﹣3y+6=0的距离d1=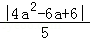
则d1+d2=a2+1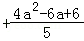 =
=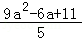
当a=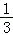 时,P到直线l1和直线l2的距离之和的最小值为2
时,P到直线l1和直线l2的距离之和的最小值为2
故选:B.
【点评】此题考查学生灵活运用抛物线的简单性质解决实际问题,灵活运用点到直线的距离公式化简求值,是一道中档题
10.(5分)某企业生产甲、乙两种产品.已知生产每吨甲产品要用A原料3吨、B原料2吨;生产每吨乙产品要用A原料1吨、B原料3吨.销售每吨甲产品可获得利润5万元、每吨乙产品可获得利润3万元.该企业在一个生产周期内消耗A原料不超过13吨、B原料不超过18吨,那么该企业可获得最大利润是( )
A.12万元B.20万元 C.25万元 D.27万元
【考点】7C:简单线性规划.菁优网版权所有
【专题】12:应用题;16:压轴题.
【分析】先设该企业生产甲产品为x吨,乙产品为y吨,列出约束条件,再根据约束条件画出可行域,设z=5x+3y,再利用z的几何意义求最值,只需求出直线z=5x+3y过可行域内的点时,从而得到z值即可.
【解答】解:设该企业生产甲产品为x吨,乙产品为y吨,则该企业可获得利润为z=5x+3y,且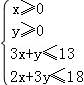
联立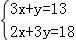 解得
解得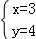
由图可知,最优解为P(3,4),
∴z的最大值为z=5×3+3×4=27(万元).
故选:D.
【点评】在解决线性规划的应用题时,其步骤为:①分析题目中相关量的关系,列出不等式组,即约束条件⇒②由约束条件画出可行域⇒③分析目标函数Z与直线截距之间的关系⇒④使用平移直线法求出最优解⇒⑤还原到现实问题中.
11.(5分)2位男生和3位女生共5位同学站成一排,若男生甲不站两端,3位女生中有且只有两位女生相邻,则不同排法的种数是( )
A.60B.48 C.42 D.36
【考点】D9:排列、组合及简单计数问题.菁优网版权所有
【专题】11:计算题;16:压轴题.
【分析】从3名女生中任取2人“捆”在一起,剩下一名女生记作B,两名男生分别记作甲、乙,则男生甲必须在A、B之间,最后再在排好的三个元素中选出四个位置插入乙.
【解答】解:从3名女生中任取2人“捆”在一起记作A,(A共有C32A22=6种不同排法),
剩下一名女生记作B,两名男生分别记作甲、乙;
则男生甲必须在A、B之间(若甲在A、B两端.则为使A、B不相邻,只有把男生乙排在A、B之间,此时就不能满足男生甲不在两端的要求)
此时共有6×2=12种排法(A左B右和A右B左)
最后再在排好的三个元素中选出四个位置插入乙,
∴共有12×4=48种不同排法.
故选:B.
【点评】本题考查的是排列问题,把排列问题包含在实际问题中,解题的关键是看清题目的实质,把实际问题转化为数学问题,解出结果以后再还原为实际问题.
12.(5分)已知函数f(x)是定义在实数集R上的不恒为零的偶函数,且对任意实数x都有xf(x+1)=(1+x)f(x),则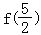 的值是( )
的值是( )
A.0B.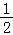 C.1 D.
C.1 D.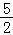
【考点】3I:奇函数、偶函数;3T:函数的值.菁优网版权所有
【专题】11:计算题;16:压轴题.
【分析】从xf(x+1)=(1+x)f(x)结构来看,要用递推的方法,先用赋值法求得 ,再由
,再由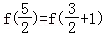 依此求解.
依此求解.
【解答】解:若x≠0,则有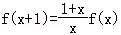 ,取
,取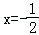 ,
,
则有:
∵f(x)是偶函数,则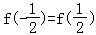
由此得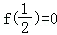
于是,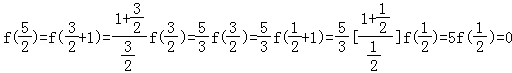
故选:A.
【点评】本题主要考查利用函数的主条件用递推的方法求函数值,这类问题关键是将条件和结论有机地结合起来,作适当变形,把握递推的规律.
二、填空题(共4小题,每小题4分,满分16分)
13.(4分)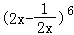 的展开式的常数项是 ﹣20 (用数字作答)
的展开式的常数项是 ﹣20 (用数字作答)
【考点】DA:二项式定理.菁优网版权所有
【分析】利用二项展开式的通项公式求出第r+1项,令x的指数为0求得常数项.
【解答】解: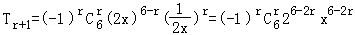 ,
,
令6﹣2r=0,得r=3
故展开式的常数项为(﹣1)3C63=﹣20
故答案为﹣20
【点评】二项展开式的通项公式是解决二项展开式的特定项问题的工具.
14.(4分)若⊙O1:x2+y2=5与⊙O2:(x﹣m)2+y2=20(m∈R)相交于A、B两点,且两圆在点A处的切线互相垂直,则线段AB的长度是 4 .
【考点】IA:两条直线垂直与倾斜角、斜率的关系;J1:圆的标准方程.菁优网版权所有
【专题】16:压轴题.
【分析】画出草图,O1A⊥AO2,有勾股定理可得m的值,再用等面积法,求线段AB的长度.
【解答】解:由题 O1(0,0)与O2:(m,0)
 ,O1A⊥AO2,
,O1A⊥AO2,
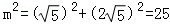 ,∴m=±5
,∴m=±5
AB=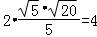
故答案为:4
【点评】本小题考查圆的标准方程、两直线的位置关系等知识,综合题.
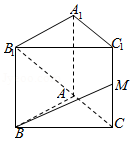
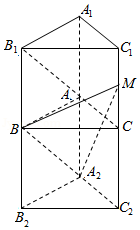
15.(4分)如图所示,已知正三棱柱ABC﹣A1B1C1的各条棱长都相等,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是 90° .
【考点】LM:异面直线及其所成的角.菁优网版权所有
【专题】11:计算题;16:压轴题.
【分析】由题意设棱长为a,补正三棱柱ABC﹣A2B2C2,构造直角三角形A2BM,解直角三角形求出BM,利用勾股定理求出A2M,从而求解.
【解答】解:设棱长为a,补正三棱柱ABC﹣A2B2C2(如图).
平移AB1至A2B,连接A2M,∠MBA2即为AB1与BM所成的角,
在△A2BM中,A2B=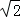 a,BM=
a,BM=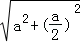 =
=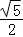 a,
a,
A2M=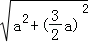 =
=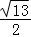 a,
a,
∴A2B2+BM2=A2M2,
∴∠MBA2=90°.
故答案为90°.
【点评】此题主要考查了异面直线及其所成的角和勾股定理的应用,计算比较复杂,要仔细的做.
16.(4分)设V是已知平面M上所有向量的集合,对于映射 ,记
,记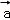 的象为
的象为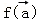 .若映射f:V→V满足:对所有
.若映射f:V→V满足:对所有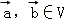 及任意实数λ,μ都有
及任意实数λ,μ都有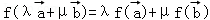 ,则f称为平面M上的线性变换.现有下列命题:
,则f称为平面M上的线性变换.现有下列命题:
①设f是平面M上的线性变换,则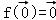
②对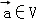 设
设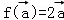 ,则f是平面M上的线性变换;
,则f是平面M上的线性变换;
③若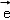 是平面M上的单位向量,对
是平面M上的单位向量,对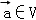 设
设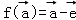 ,则f是平面M上的线性变换;
,则f是平面M上的线性变换;
④设f是平面M上的线性变换,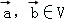 ,若
,若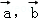 共线,则
共线,则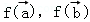 也共线.
也共线.
其中真命题是 ①②④ (写出所有真命题的序号)
【考点】3C:映射;96:平行向量(共线).菁优网版权所有
【专题】16:压轴题.
【分析】本题考查的知识点的演绎推理,由已知中,若映射f:V→V满足:对所有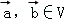 及任意实数λ,μ都有
及任意实数λ,μ都有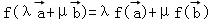 ,则f称为平面M上的线性变换.我们根据其定义对题目中的四个结论进行判断,即可得到结论.
,则f称为平面M上的线性变换.我们根据其定义对题目中的四个结论进行判断,即可得到结论.
【解答】解:令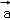 =
=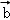 =
= ,λ=μ=1,
,λ=μ=1,
由题有f(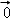 )=2f(
)=2f(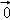 )⇒f(
)⇒f(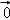 )=
)= ,故①正确;
,故①正确;
由题f(λ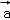 +μ
+μ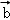 )=2(λ
)=2(λ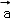 +μ
+μ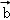 ),
),
λf( )+μf(
)+μf(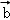 )=2λ
)=2λ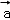 +2μ
+2μ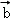 )=2(λ
)=2(λ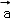 +μ
+μ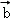 ),
),
即f(λ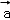 +μ
+μ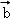 )=λf(
)=λf(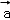 )+μf(
)+μf(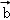 ),故②正确;
),故②正确;
由题f(λ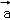 +μ
+μ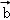 )=λ
)=λ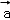 +μ
+μ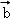 ﹣
﹣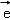 ,
,
λf(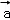 )+μf(
)+μf(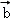 )=λ
)=λ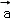 ﹣
﹣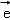 +μ
+μ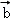 ﹣
﹣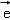 ,,
,,
即f(λ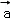 +μ
+μ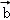 ≠λf(
≠λf(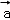 )+μf(
)+μf(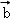 ),故③不正确;
),故③不正确;
由题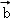 =λ
=λ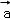 ,f(
,f(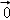 )=f(
)=f(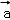 ﹣λ
﹣λ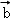 )=f(
)=f(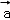 )﹣λf(
)﹣λf(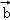 )
)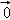 ⇒f(
⇒f(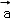 )=λf(
)=λf(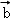 ),
),
即f( ),f(
),f(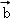 )也共线,故④正确;
)也共线,故④正确;
故答案为:①②④
【点评】演绎推理的主要形式就是由大前提、小前提推出结论的三段论推理.三段论推理的依据用集合论的观点来讲就是:若集合M的所有元素都具有性质P,S是M的子集,那么S中所有元素都具有性质P.三段论的公式中包含三个判断:第一个判断称为大前提,它提供了一个一般的原理;第二个判断叫小前提,它指出了一个特殊情况;这两个判断联合起来,揭示了一般原理和特殊情况的内在联系,从而产生了第三个判断结论.演绎推理是一种必然性推理,演绎推理的前提与结论之间有蕴涵关系.因而,只要前提是真实的,推理的形式是正确的,那么结论必定是真实的,但错误的前提可能导致错误的结论.
三、解答题(共6小题,满分74分)
17.(12分)在△ABC中,A、B为锐角,角A、B、C所对的边分别为a、b、c,且cos2A=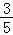 ,sinB=
,sinB=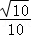 .
.
(1)求A+B的值;
(2)若a﹣b=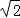 ﹣1,求a、b、c的值.
﹣1,求a、b、c的值.
【考点】GL:三角函数中的恒等变换应用;HP:正弦定理.菁优网版权所有
【分析】(1)根据同角三角函数的基本关系可得cosB的值,再由余弦函数的二倍角公式可得sinA和cosA的值,最后根据两角和的余弦公式可得答案.
(2)根据(1)可求出角C的值,进而得到角C的正弦值,再由正弦定理可求出abc的值.
【解答】解:(1)∵A、B为锐角,sinB=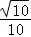 ,
,
∴cosB=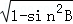 =
=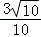 .
.
又cos2A=1﹣2sin2A=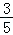 ,
,
∴sinA=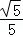 ,cosA=
,cosA=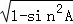 =
=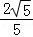 .
.
∴cos(A+B)=cosAcosB﹣sinAsinB=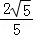 ×
×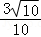 ﹣
﹣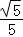 ×
× =
=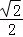 .
.
∵0<A+B<π,∴A+B=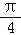 .
.
(2)由(1)知C=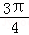 ,∴sinC=
,∴sinC=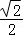 .
.
由正弦定理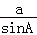 =
=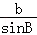 =
=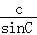 得
得
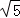 a=
a=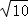 b=
b=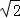 c,即a=
c,即a=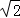 b,c=
b,c=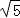 b.
b.
∵a﹣b=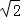 ﹣1,∴
﹣1,∴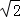 b﹣b=
b﹣b=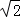 ﹣1,∴b=1.
﹣1,∴b=1.
∴a= ,c=
,c= .
.
【点评】本小题主要考查同角三角函数间的关系、两角和差的三角函数、二倍角公式、正弦定理等基础知识及基本运算能力.
18.(12分)为振兴旅游业,四川省2009年面向国内发行总量为2000万张的熊猫优惠卡,向省外人士发行的是熊猫金卡(简称金卡),向省内人士发行的是熊猫银卡(简称银卡).某旅游公司组织了一个有36名游客的旅游团到四川名胜旅游,其中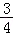 是省外游客,其余是省内游客.在省外游客中有
是省外游客,其余是省内游客.在省外游客中有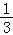 持金卡,在省内游客中有
持金卡,在省内游客中有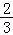 持银卡.
持银卡.
(Ⅰ)在该团中随机采访3名游客,求恰有1人持金卡且持银卡者少于2人的概率;
(Ⅱ)在该团的境内游客中随机采访3名游客,设其中持银卡人数为随机变量ξ,求ξ的分布列及数学期望Eξ.
【考点】C8:相互独立事件和相互独立事件的概率乘法公式;CH:离散型随机变量的期望与方差.菁优网版权所有
【专题】11:计算题.
【分析】(Ⅰ)由题意得,省外游客有27人,其中9人持金卡;省内游客有9人,其中6人持银卡.记出事件,表示出事件的概率,根据互斥事件的概率公式,得到结论.
(Ⅱ)在该团的境内游客中随机采访3名游客,其中持银卡人数为随机变量ξ,则得到ξ的可能取值,做出变量在不同取值时对应的概率,写出分布列和期望.
【解答】解:(Ⅰ)∵现有一个由36名游客组成的旅游团到上海参观旅游,
其中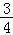 是省外游客,其余是省内游客.
是省外游客,其余是省内游客.
∴由题意得,省外游客有27人,
其中9人持金卡;境内游客有9人,其中6人持银卡.
设事件B为“采访该团3人中,恰有1人持金卡且持银卡者少于2人”,
事件A1为“采访该团3人中,1人持金卡,0人持银卡”,
事件A2为“采访该团3人中,1人持金卡,1人持银卡”.
P(B)=P(A1)+P(A2)

=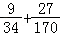
=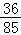
所以,在该团中随机采访3人,
恰有1人持金卡且持银卡者少于2人的概率是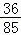 .
.
(Ⅱ)ξ的可能取值为0,1,2,3
P(ξ=0)= ;,P(ξ=1)=
;,P(ξ=1)=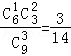 .
.
P=(ξ=2)=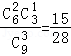 ,P(ξ=3)=
,P(ξ=3)=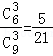 ,
,
所以ξ的分布列为
ζ | 0 | 1 | 2 | 3 |
P | | | | |
∴Eξ=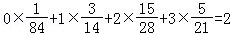 .
.
【点评】考查运用概率知识解决实际问题的能力,注意满足独立重复试验的条件,解题过程中判断概率的类型是难点也是重点,这种题目高考必考,应注意解题的格式.
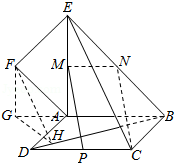
19.(12分)如图,正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直,△ABE是等腰直角三角形,AB=AE,FA=FE,∠AEF=45°
(I)求证:EF⊥平面BCE;
(Ⅱ)设线段CD、AE的中点分别为P、M,求证:PM∥平面BCE;
(Ⅲ)求二面角F﹣BD﹣A的大小.
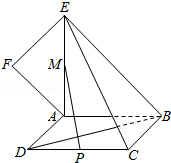
【考点】LQ:平面与平面之间的位置关系;LS:直线与平面平行;LY:平面与平面垂直;MJ:二面角的平面角及求法.菁优网版权所有
【专题】11:计算题;14:证明题.
【分析】(1)欲证EF⊥平面BCE,根据线面垂直的判定定理可知只需证EF⊥BE,BC⊥EF,BC∩BE=B,根据条件很显然;
(2)取BE的中点N,连接CN,MN,易证PM∥CN,根据线面平行的判定定理很快得证;
(3)作FG⊥AB,交BA的延长线于G,作GH⊥BD于H,连接FH,易证∠FHG为二面角F﹣BD﹣A的平面角,在Rt△FGH中求出此角即可.
【解答】解:因为平面ABEF⊥平面ABCD,BC⊂平面ABCD,BC⊥AB,平面ABEF∩平面ABCD=AB,
所以BC⊥平面ABEF
所以BC⊥EF
因为△ABE为等腰直角三角形,AB=AE,
所以∠AEB=45°,
又因为∠AEF=45,
所以∠FEB=90°,即EF⊥BE
因为BC⊂平面ABCD,BE⊂平面BCE,
BC∩BE=B
所以EF⊥平面BCE
( II)取BE的中点N,连接CN,MN,则MN=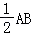 =PC
=PC
∴PMNC为平行四边形,所以PM∥CN
∵CN在平面BCE内,PM不在平面BCE内,
∴PM∥平面BCE.
(III)由EA⊥AB,平面ABEF⊥平面ABCD,易知EA⊥平面ABCD、
作FG⊥AB,交BA的延长线于G,则FG∥EA、从而FG⊥平面ABCD,
作GH⊥BD于H,连接FH,则由三垂线定理知BD⊥FH、
∴∠FHG为二面角F﹣BD﹣A的平面角、
∵FA=FE,∠AEF=45°,
∠AEF=90°,∠FAG=45°、
设AB=1,则AE=1,AF=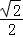 ,则
,则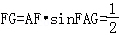
在Rt△BGH中,∠GBH=45°,BG=AB+AG=1+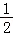 =
= ,
,
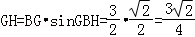 ,
,
在Rt△FGH中,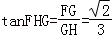 ,
,
∴二面角F﹣BD﹣A的大小为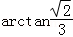
【点评】本题主要考查了平面与平面之间的位置关系,考查空间想象能力、运算能力和推理论证能力,属于基础题.
20.(12分)已知椭圆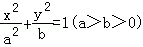 的左、右焦点分别为F1、F2,离心率
的左、右焦点分别为F1、F2,离心率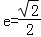 ,右准线方程为x=2.
,右准线方程为x=2.
(1)求椭圆的标准方程;
(2)过点F1的直线l与该椭圆交于M、N两点,且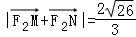 ,求直线l的方程.
,求直线l的方程.
【考点】IG:直线的一般式方程与直线的性质;K3:椭圆的标准方程;KH:直线与圆锥曲线的综合.菁优网版权所有
【专题】11:计算题;16:压轴题.
【分析】(1)由已知得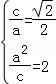 ,解得
,解得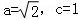 ,由此能得到所求椭圆的方程.
,由此能得到所求椭圆的方程.
(2)由题意知F1(﹣1,0)、F2(1,0),①若直线l的斜率不存在,
则直线l的方程为x=﹣1,由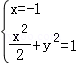 得
得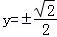
设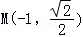 、
、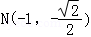 ,
,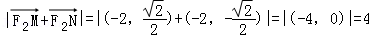 ,这与已知相矛盾.
,这与已知相矛盾.
②若直线l的斜率存在,设直线直线l的斜率为k,则直线l的方程为y=k(x+1),设M(x1,y1)、N(x2,y2),联立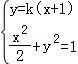 ,消元得(1+2k2)x2+4k2x+2k2﹣2=0.再由根与系数的关系进行求解.
,消元得(1+2k2)x2+4k2x+2k2﹣2=0.再由根与系数的关系进行求解.
【解答】解:(1)由已知得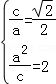 ,
,
解得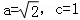
∴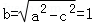 ∴所求椭圆的方程为
∴所求椭圆的方程为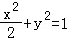
( 2)由(1)得F1(﹣1,0)、F2(1,0)
①若直线l的斜率不存在,则直线l的方程为x=﹣1,
由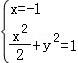 得
得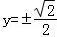
设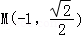 、
、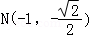 ,
,
∴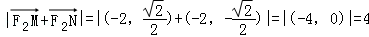 ,这与已知相矛盾.
,这与已知相矛盾.
②若直线l的斜率存在,设直线直线l的斜率为k,则直线l的方程为y=k(x+1),
设M(x1,y1)、N(x2,y2),
联立 ,消元得(1+2k2)x2+4k2x+2k2﹣2=0
,消元得(1+2k2)x2+4k2x+2k2﹣2=0
∴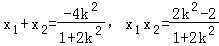 ,
,
∴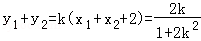 .
.
又∵
∴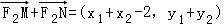
∴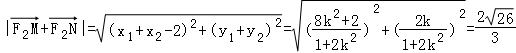
化简得40k4﹣23k2﹣17=0
解得k2=1或k2=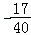 (舍去)
(舍去)
∴k=±1
∴所求直线l的方程为y=x+1或y=﹣x﹣1
【点评】本题考查直线和圆锥曲线的综合应用,解题时要认真审题,合理解答.
21.(12分)已知a>0且a≠1,函数f(x)=loga(1﹣ax).
(1)求函数f(x)的定义域,并判断f(x)的单调性;
(2)若n∈N*,求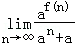 ;
;
(3)当a=e(e为自然对数的底数)时,设h(x)=(1﹣ef(x))(x2﹣m+1).若函数的极值存在,求实数m的取值范围以及函数h(x)的极值.
【考点】4K:对数函数的定义域;4O:对数函数的单调性与特殊点;6D:利用导数研究函数的极值;6F:极限及其运算.菁优网版权所有
【专题】11:计算题;16:压轴题.
【分析】(1)据对数函数的真数大于0,列出不等式求出定义域;求出导函数,利用导函数大于0函数得到递增;导函数小于0函数单调递减.
(2)求出f(n)代入极限式,利用特殊函数的极限值求出极限.
(3)求出导函数,令导函数为0,导函数是否有根进行分类讨论;导函数的根是否在定义域内再一次引起分类讨论,利用极值的定义求出极值.
【解答】解:(1)由题意知,1﹣ax>0
所以当0<a<1时,f(x)的定义域是(0,+∞),a>1时,f(x)的定义域是(﹣∞,0),
f′(x)=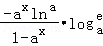 =
=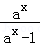
当0<a<1时,x∈(0,+∞),因为ax﹣1<0,ax>0,故f'(x)<0,所以f(x)是减函数.
当a>1时,x∈(﹣∞,0),因为ax﹣1<0,ax>0,故f'(x)<0,所以f(x)是减函数.
(2)因为f(n)=loga(1﹣an),所以af(n)=1﹣an,由函数定义域知1﹣an>0,因为n是正整数,故0<a<1,
所以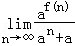 =
=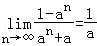 .
.
(3)h(x)=ex(x2﹣m+1)(x<0),所以h'(x)=ex(x2+2x﹣m+1),令h'(x)=0,即x2+2x﹣m+1=0,由题意应有△≥0,即m≥0.
①当m=0时,h'(x)=0有实根x=﹣1,在x=﹣1点左右两侧均有h'(x)>0,故h(x)无极值.
②当0<m<1时,h'(x)=0有两个实根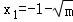 ,
,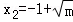 .当x变化时,h'(x)的变化情况如下表:
.当x变化时,h'(x)的变化情况如下表:
x | (﹣∞,x1) | x1 | (x1,x2) | x2 | (x2,0) |
h′(x) | + | 0 | ﹣ | 0 | + |
h(x) | 递增 | 极大值 | 递减 | 极小值 | 递增 |
∴h(x)的极大值为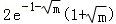 ,h(x)的极小值为
,h(x)的极小值为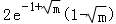 .
.
③当m≥1时,h'(x)=0在定义域内有一个实根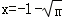 .
.
同上可得h(x)的极大值为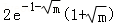 .
.
综上所述,m∈(0,+∞)时,函数h(x)有极值.
当0<m<1时,h(x)的极大值为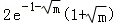 ,h(x)的极小值为
,h(x)的极小值为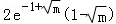 .
.
当m≥1时,h(x)的极大值为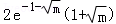 .
.
【点评】本题考查利用导数的符号讨论函数的单调性;利用导数研究函数的极值;在含参数的函数中需要分类讨论.
22.(14分)设数列{an}的前n项和为Sn,对任意的正整数n,都有an=5Sn+1成立,记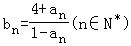 .
.
(Ⅰ)求数列{bn}的通项公式;
(Ⅱ)记cn=b2n﹣b2n﹣1(n∈N*),设数列{cn}的前n项和为Tn,求证:对任意正整数n都有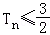 ;
;
(Ⅲ)设数列{bn}的前n项和为Rn.已知正实数λ满足:对任意正整数nRn≤λn恒成立,求λ的最小值.
【考点】8E:数列的求和;8H:数列递推式;8K:数列与不等式的综合.菁优网版权所有
【专题】15:综合题;16:压轴题.
【分析】(Ⅰ)由题设条件能导出an+1﹣an=5an+1,即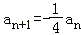 ,所以
,所以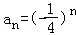 ,∴
,∴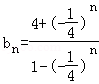 .
.
(Ⅱ)由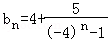 ,知
,知 =
=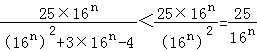 ,当n=1时,
,当n=1时, ;当n≥2时,
;当n≥2时,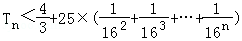
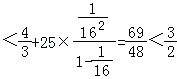 .
.
(Ⅲ)由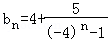 知Rn=b1+b2+…+b2k+1=
知Rn=b1+b2+…+b2k+1=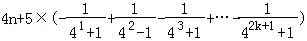 =
=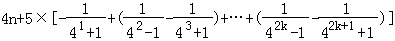 >4n﹣1.由此入手能推导出正实数λ的最小值为4.
>4n﹣1.由此入手能推导出正实数λ的最小值为4.
【解答】解:(Ⅰ)当n=1时,a1=5a1+1,∴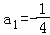
又∵an=5Sn+1,an+1=5Sn+1+1
∴an+1﹣an=5an+1,即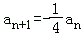
∴数列an成等比数列,其首项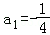 ,公比是
,公比是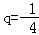
∴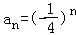
∴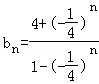
(Ⅱ)由(Ⅰ)知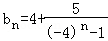
∴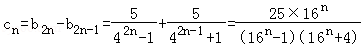
=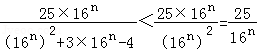
又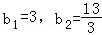 ,∴
,∴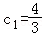
当n=1时,
当n≥2时,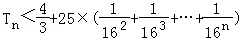
=
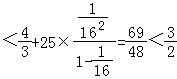 ,故所证结论成立
,故所证结论成立
(Ⅲ)由(Ⅰ)知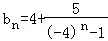
一方面,已知Rn≤λn恒成立,取n为大于1的奇数时,设n=2k+1(k∈N+)
则Rn=b1+b2+…+b2k+1
=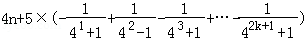
=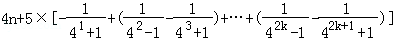
>4n﹣1
∴λn≥Rn>4n﹣1,即(λ﹣4)n>﹣1对一切大于1的奇数n恒成立
∴λ≥4否则,(λ﹣4)n>﹣1只对满足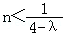 的正奇数n成立,矛盾.
的正奇数n成立,矛盾.
另一方面,当λ=4时,对一切的正整数n都有Rn≤4n
事实上,对任意的正整数k,有
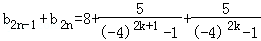
=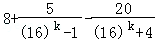
=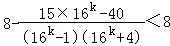
∴当n为偶数时,设n=2m(m∈N+)
则Rn=(b1+b2)+(b3+b4)+…+(b2n﹣1+b2n)
<8m=4n
当n为奇数时,设n=2m﹣1(m∈N+)
则Rn=(b1+b2)+(b3+b4)+…+(b2n﹣3+b2n﹣2)+b2n﹣1
<8(m﹣1)+4=8m﹣4=4n
∴对一切的正整数n,都有Rn≤4n
综上所述,正实数λ的最小值为4
【点评】本题主要考查数列、不等式等基础知识、考查化归思想、分类整合思想,以及推理论证、分析与解决问题的能力.