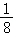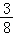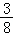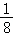2014年四川省高考数学试卷(理科)(含解析版)

2014年四川省高考数学试卷(理科)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给处的四个选项中,只有一项是符合题目要求的.
1.(5分)已知集合A={x|x2﹣x﹣2≤0},集合B为整数集,则A∩B=( )
A.{﹣1,0,1,2}B.{﹣2,﹣1,0,1}
C.{0,1} D.{﹣1,0}
2.(5分)在x(1+x)6的展开式中,含x3项的系数为( )
A.30B.20 C.15 D.10
3.(5分)为了得到函数y=sin(2x+1)的图象,只需把y=sin2x的图象上所有的点( )
A.向左平行移动个单位长度B.向右平行移动 个单位长度
个单位长度
C.向左平行移动1个单位长度D.向右平行移动1个单位长度
4.(5分)若a>b>0,c<d<0,则一定有( )
A.>B.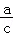 <
<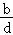 C.
C.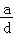 >
>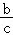 D.
D.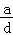 <
<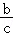
5.(5分)执行如图所示的程序框图,若输入的x,y∈R,那么输出的S的最大值为( )
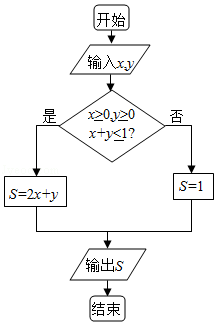
A.0B.1 C.2 D.3
6.(5分)六个人从左至右排成一行,最左端只能排甲或乙,最右端不能排甲,则不同的排法共有( )
A.192种B.216种 C.240种 D.288种
7.(5分)平面向量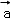 =(1,2),
=(1,2),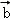 =(4,2),
=(4,2),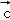 =m
=m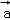 +
+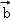 (m∈R),且
(m∈R),且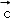 与
与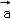 的夹角等于
的夹角等于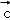 与
与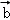 的夹角,则m=( )
的夹角,则m=( )
A.﹣2B.﹣1 C.1 D.2
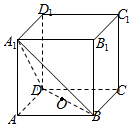
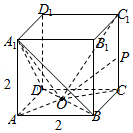
8.(5分)如图,在正方体ABCD﹣A1B1C1D1中,点O为线段BD的中点,设点P在线段CC1上,直线OP与平面A1BD所成的角为α,则sinα的取值范围是( )
A.[,1]B.[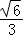 ,1] C.[
,1] C.[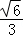 ,
,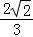 ] D.[
] D.[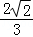 ,1]
,1]
9.(5分)已知f(x)=ln(1+x)﹣ln(1﹣x),x∈(﹣1,1).现有下列命题:
①f(﹣x)=﹣f(x);
②f(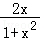 )=2f(x)
)=2f(x)
③|f(x)|≥2|x|
其中的所有正确命题的序号是( )
A.①②③B.②③ C.①③ D.①②
10.(5分)已知F为抛物线y2=x的焦点,点A,B在该抛物线上且位于x轴的两侧,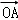 •
•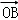 =2(其中O为坐标原点),则△ABO与△AFO面积之和的最小值是( )
=2(其中O为坐标原点),则△ABO与△AFO面积之和的最小值是( )
A.2B.3 C.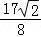 D.
D.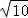
二、填空题:本大题共5小题,每小题5分,共25分
11.(5分)复数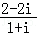 = .
= .
12.(5分)设f(x)是定义在R上的周期为2的函数,当x∈[﹣1,1)时,f(x)=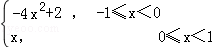 ,则f(
,则f(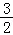 )= .
)= .
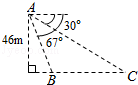
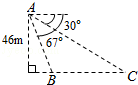
13.(5分)如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为67°,30°,此时气球的高是46m,则河流的宽度BC约等于 m.(用四舍五入法将结果精确到个位.参考数据:sin67°≈0.92,cos67°≈0.39,sin37°≈0.60,cos37°≈0.80,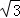 ≈1.73)
≈1.73)
14.(5分)设m∈R,过定点A的动直线x+my=0和过定点B的动直线mx﹣y﹣m+3=0交于点P(x,y).则|PA|•|PB|的最大值是 .
15.(5分)以A表示值域为R的函数组成的集合,B表示具有如下性质的函数φ(x)组成的集合:对于函数φ(x),存在一个正数M,使得函数φ(x)的值域包含于区间[﹣M,M].例如,当φ1(x)=x3,φ2(x)=sinx时,φ1(x)∈A,φ2(x)∈B.现有如下命题:
①设函数f(x)的定义域为D,则“f(x)∈A”的充要条件是“∀b∈R,∃a∈D,f(a)=b”;
②函数f(x)∈B的充要条件是f(x)有最大值和最小值;
③若函数f(x),g(x)的定义域相同,且f(x)∈A,g(x)∈B,则f(x)+g(x)∉B.
④若函数f(x)=aln(x+2)+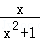 (x>﹣2,a∈R)有最大值,则f(x)∈B.
(x>﹣2,a∈R)有最大值,则f(x)∈B.
其中的真命题有 .(写出所有真命题的序号)
三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.
16.(12分)已知函数f(x)=sin(3x+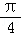 ).
).
(1)求f(x)的单调递增区间;
(2)若α是第二象限角,f(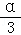 )=
)=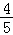 cos(α+
cos(α+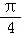 )cos2α,求cosα﹣sinα的值.
)cos2α,求cosα﹣sinα的值.
17.(12分)一款击鼓小游戏的规则如下:每盘游戏都需要击鼓三次,每次击鼓要么出现一次音乐,要么不出现音乐:每盘游戏击鼓三次后,出现一次音乐获得10分,出现两次音乐获得20分,出现三次音乐获得100分,没有出现音乐则扣除200分(即获得﹣200分).设每次击鼓出现音乐的概率为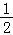 ,且各次击鼓出现音乐相互独立.
,且各次击鼓出现音乐相互独立.
(1)设每盘游戏获得的分数为X,求X的分布列;
(2)玩三盘游戏,至少有一盘出现音乐的概率是多少?
(3)玩过这款游戏的许多人都发现.若干盘游戏后,与最初分数相比,分数没有增加反而减少了.请运用概率统计的相关知识分析分数减少的原因.
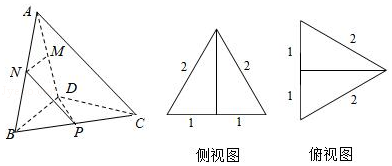
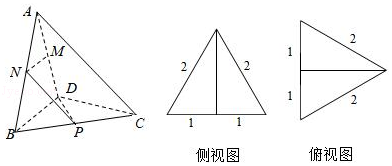
18.(12分)三棱锥A﹣BCD及其侧视图、俯视图如图所示,设M,N分别为线段AD,AB的中点,P为线段BC上的点,且MN⊥NP.
(1)证明:P是线段BC的中点;
(2)求二面角A﹣NP﹣M的余弦值.
19.(12分)设等差数列{an}的公差为d,点(an,bn)在函数f(x)=2x的图象上(n∈N*).
(1)若a1=﹣2,点(a8,4b7)在函数f(x)的图象上,求数列{an}的前n项和Sn;
(2)若a1=1,函数f(x)的图象在点(a2,b2)处的切线在x轴上的截距为2﹣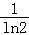 ,求数列{
,求数列{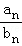 }的前n项和Tn.
}的前n项和Tn.
20.(13分)已知椭圆C: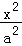 +
+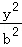 =1(a>b>0)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
=1(a>b>0)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(1)求椭圆C的标准方程;
(2)设F为椭圆C的左焦点,T为直线x=﹣3上任意一点,过F作TF的垂线交椭圆C于点P,Q.
①证明:OT平分线段PQ(其中O为坐标原点);
②当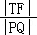 最小时,求点T的坐标.
最小时,求点T的坐标.
21.(14分)已知函数f(x)=ex﹣ax2﹣bx﹣1,其中a,b∈R,e=2.71828…为自然对数的底数.
(1)设g(x)是函数f(x)的导函数,求函数g(x)在区间[0,1]上的最小值;
(2)若f(1)=0,函数f(x)在区间(0,1)内有零点,求a的取值范围.
2014年四川省高考数学试卷(理科)
参考答案与试题解析
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给处的四个选项中,只有一项是符合题目要求的.
1.(5分)已知集合A={x|x2﹣x﹣2≤0},集合B为整数集,则A∩B=( )
A.{﹣1,0,1,2}B.{﹣2,﹣1,0,1}
C.{0,1} D.{﹣1,0}
【考点】1E:交集及其运算.菁优网版权所有
【专题】11:计算题.
【分析】计算集合A中x的取值范围,再由交集的概念,计算可得.
【解答】解:A={x|﹣1≤x≤2},B=Z,
∴A∩B={﹣1,0,1,2}.
故选:A.
【点评】本题属于容易题,集合知识是高中部分的基础知识,也是基础工具,高考中涉及到对集合的基本考查题,一般都比较容易,且会在选择题的前几题,考生只要够细心,一般都能拿到分.
2.(5分)在x(1+x)6的展开式中,含x3项的系数为( )
A.30B.20 C.15 D.10
【考点】DA:二项式定理.菁优网版权所有
【专题】5P:二项式定理.
【分析】利用二项展开式的通项公式求出(1+x)6的第r+1项,令x的指数为2求出展开式中x2的系数.然后求解即可.
【解答】解:(1+x)6展开式中通项Tr+1=C6rxr,
令r=2可得,T3=C62x2=15x2,
∴(1+x)6展开式中x2项的系数为15,
在x(1+x)6的展开式中,含x3项的系数为:15.
故选:C.
【点评】本题考查二项展开式的通项的简单直接应用.牢记公式是基础,计算准确是关键.
3.(5分)为了得到函数y=sin(2x+1)的图象,只需把y=sin2x的图象上所有的点( )
A.向左平行移动个单位长度B.向右平行移动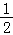 个单位长度
个单位长度
C.向左平行移动1个单位长度D.向右平行移动1个单位长度
【考点】HJ:函数y=Asin(ωx+φ)的图象变换.菁优网版权所有
【专题】57:三角函数的图像与性质.
【分析】根据 y=sin(2x+1)=sin2(x+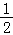 ),利用函数y=Asin(ωx+φ)的图象变换规律,得出结论.
),利用函数y=Asin(ωx+φ)的图象变换规律,得出结论.
【解答】解:∵y=sin(2x+1)=sin2(x+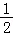 ),∴把y=sin2x的图象上所有的点向左平行移动
),∴把y=sin2x的图象上所有的点向左平行移动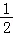 个单位长度,
个单位长度,
即可得到函数y=sin(2x+1)的图象,
故选:A.
【点评】本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.
4.(5分)若a>b>0,c<d<0,则一定有( )
A.>B.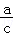 <
<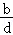 C.
C.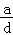 >
>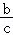 D.
D.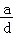 <
<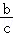
【考点】R3:不等式的基本性质.菁优网版权所有
【专题】59:不等式的解法及应用.
【分析】利用特例法,判断选项即可.
【解答】解:不妨令a=3,b=1,c=﹣3,d=﹣1,
则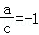 ,
,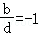 ,∴A、B不正确;
,∴A、B不正确;
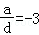 ,
,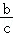 =﹣
=﹣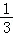 ,
,
∴C不正确,D正确.
解法二:
∵c<d<0,
∴﹣c>﹣d>0,
∵a>b>0,
∴﹣ac>﹣bd,
∴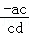
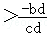 ,
,
∴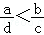 .
.
故选:D.
【点评】本题考查不等式比较大小,特值法有效,导数计算正确.
5.(5分)执行如图所示的程序框图,若输入的x,y∈R,那么输出的S的最大值为( )
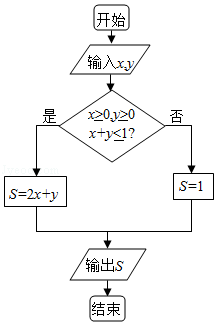
A.0B.1 C.2 D.3
【考点】7C:简单线性规划;E9:程序框图的三种基本逻辑结构的应用.菁优网版权所有
【专题】5K:算法和程序框图.
【分析】算法的功能是求可行域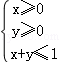 内,目标函数S=2x+y的最大值,画出可行域,求得取得最大值的点的坐标,得出最大值.
内,目标函数S=2x+y的最大值,画出可行域,求得取得最大值的点的坐标,得出最大值.
【解答】解:由程序框图知:算法的功能是求可行域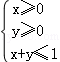 内,目标还是S=2x+y的最大值,
内,目标还是S=2x+y的最大值,
画出可行域如图:
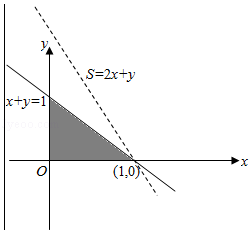
当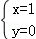 时,S=2x+y的值最大,且最大值为2.
时,S=2x+y的值最大,且最大值为2.
故选:C.
【点评】本题借助选择结构的程序框图考查了线性规划问题的解法,根据框图的流程判断算法的功能是解题的关键.
6.(5分)六个人从左至右排成一行,最左端只能排甲或乙,最右端不能排甲,则不同的排法共有( )
A.192种B.216种 C.240种 D.288种
【考点】D9:排列、组合及简单计数问题.菁优网版权所有
【专题】12:应用题;5O:排列组合.
【分析】分类讨论,最左端排甲;最左端只排乙,最右端不能排甲,根据加法原理可得结论.
【解答】解:最左端排甲,共有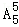 =120种,最左端只排乙,最右端不能排甲,有
=120种,最左端只排乙,最右端不能排甲,有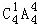 =96种,
=96种,
根据加法原理可得,共有120+96=216种.
故选:B.
【点评】本题考查排列、组合及简单计数问题,考查学生的计算能力,属于基础题.
7.(5分)平面向量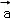 =(1,2),
=(1,2),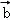 =(4,2),
=(4,2),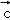 =m
=m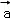 +
+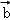 (m∈R),且
(m∈R),且 与
与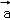 的夹角等于
的夹角等于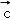 与
与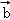 的夹角,则m=( )
的夹角,则m=( )
A.﹣2B.﹣1 C.1 D.2
【考点】9S:数量积表示两个向量的夹角.菁优网版权所有
【专题】5A:平面向量及应用.
【分析】由已知求出向量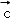 的坐标,再根据
的坐标,再根据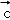 与
与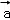 的夹角等于
的夹角等于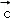 与
与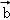 的夹角,代入夹角公式,构造关于m的方程,解方程可得答案.
的夹角,代入夹角公式,构造关于m的方程,解方程可得答案.
【解答】解:∵向量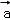 =(1,2),
=(1,2),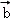 =(4,2),
=(4,2),
∴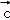 =m
=m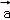 +
+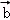 =(m+4,2m+2),
=(m+4,2m+2),
又∵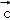 与
与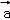 的夹角等于
的夹角等于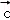 与
与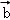 的夹角,
的夹角,
∴ =
=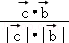 ,
,
∴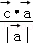 =
=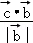 ,
,
∴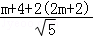 =
=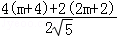 ,
,
解得m=2,
故选:D.
【点评】本题考查的知识点是数量积表示两个向量的夹角,难度中档.
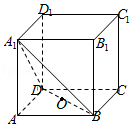
8.(5分)如图,在正方体ABCD﹣A1B1C1D1中,点O为线段BD的中点,设点P在线段CC1上,直线OP与平面A1BD所成的角为α,则sinα的取值范围是( )
A.[,1]B.[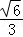 ,1] C.[
,1] C.[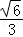 ,
,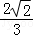 ] D.[
] D.[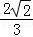 ,1]
,1]
【考点】MI:直线与平面所成的角.菁优网版权所有
【专题】5G:空间角.
【分析】由题意可得:直线OP于平面A1BD所成的角α的取值范围是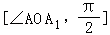 ∪
∪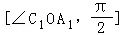 .再利用正方体的性质和直角三角形的边角关系即可得出.
.再利用正方体的性质和直角三角形的边角关系即可得出.
【解答】解:由题意可得:直线OP于平面A1BD所成的角α的取值范围是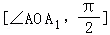 ∪
∪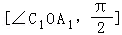 .
.
不妨取AB=2.
在Rt△AOA1中,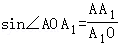 =
=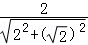 =
=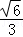 .
.
sin∠C1OA1=sin(π﹣2∠AOA1)=sin2∠AOA1=2sin∠AOA1cos∠AOA1=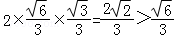 ,
,
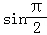 =1.
=1.
∴sinα的取值范围是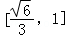 .
.
故选:B.
【点评】本题考查了正方体的性质和直角三角形的边角关系、线面角的求法,考查了推理能力,属于中档题.
9.(5分)已知f(x)=ln(1+x)﹣ln(1﹣x),x∈(﹣1,1).现有下列命题:
①f(﹣x)=﹣f(x);
②f(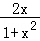 )=2f(x)
)=2f(x)
③|f(x)|≥2|x|
其中的所有正确命题的序号是( )
A.①②③B.②③ C.①③ D.①②
【考点】2K:命题的真假判断与应用.菁优网版权所有
【专题】51:函数的性质及应用;5L:简易逻辑.
【分析】根据已知中函数的解析式,结合对数的运算性质,分别判断三个结论的真假,最后综合判断结果,可得答案.
【解答】解:∵f(x)=ln(1+x)﹣ln(1﹣x),x∈(﹣1,1),
∴f(﹣x)=ln(1﹣x)﹣ln(1+x)=﹣f(x),即①正确;
f(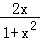 )=ln(1+
)=ln(1+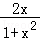 )﹣ln(1﹣
)﹣ln(1﹣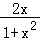 )=ln(
)=ln(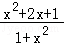 )﹣ln(
)﹣ln(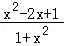 )=ln(
)=ln(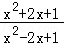 )=ln[(
)=ln[(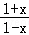 )2]=2ln(
)2]=2ln(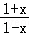 )=2[ln(1+x)﹣ln(1﹣x)]=2f(x),故②正确;
)=2[ln(1+x)﹣ln(1﹣x)]=2f(x),故②正确;
当x∈[0,1)时,|f(x)|≥2|x|⇔f(x)﹣2x≥0,令g(x)=f(x)﹣2x=ln(1+x)﹣ln(1﹣x)﹣2x(x∈[0,1))
∵g′(x)=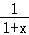 +
+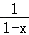 ﹣2=
﹣2=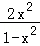 ≥0,∴g(x)在[0,1)单调递增,g(x)=f(x)﹣2x≥g(0)=0,
≥0,∴g(x)在[0,1)单调递增,g(x)=f(x)﹣2x≥g(0)=0,
又f(x)≥2x,又f(x)与y=2x为奇函数,所以|f(x)|≥2|x|成立,故③正确;
故正确的命题有①②③,
故选:A.
【点评】本题以命题的真假判断为载体,考查了对数的运算性质,代入法求函数的解析式等知识点,难度中档.
10.(5分)已知F为抛物线y2=x的焦点,点A,B在该抛物线上且位于x轴的两侧,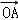 •
•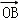 =2(其中O为坐标原点),则△ABO与△AFO面积之和的最小值是( )
=2(其中O为坐标原点),则△ABO与△AFO面积之和的最小值是( )
A.2B.3 C.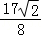 D.
D.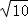
【考点】K8:抛物线的性质.菁优网版权所有
【专题】5E:圆锥曲线中的最值与范围问题.
【分析】可先设直线方程和点的坐标,联立直线与抛物线的方程得到一个一元二次方程,再利用韦达定理及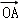 •
•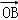 =2消元,最后将面积之和表示出来,探求最值问题.
=2消元,最后将面积之和表示出来,探求最值问题.
【解答】解:设直线AB的方程为:x=ty+m,点A(x1,y1),B(x2,y2),
直线AB与x轴的交点为M(m,0),
由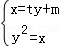 ⇒y2﹣ty﹣m=0,根据韦达定理有y1•y2=﹣m,
⇒y2﹣ty﹣m=0,根据韦达定理有y1•y2=﹣m,
∵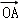 •
•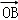 =2,∴x1•x2+y1•y2=2,
=2,∴x1•x2+y1•y2=2,
结合 及
及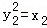 ,得
,得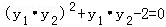 ,
,
∵点A,B位于x轴的两侧,∴y1•y2=﹣2,故m=2.
不妨令点A在x轴上方,则y1>0,又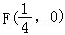 ,
,
∴S△ABO+S△AFO═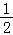 ×2×(y1﹣y2)+
×2×(y1﹣y2)+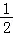 ×
×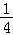 y1,
y1,
=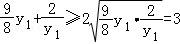 .
.
当且仅当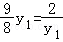 ,即
,即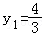 时,取“=”号,
时,取“=”号,
∴△ABO与△AFO面积之和的最小值是3,
故选:B.
【点评】求解本题时,应考虑以下几个要点:
1、联立直线与抛物线的方程,消x或y后建立一元二次方程,利用韦达定理与已知条件消元,这是处理此类问题的常见模式.
2、求三角形面积时,为使面积的表达式简单,常根据图形的特征选择适当的底与高.
3、利用基本不等式时,应注意“一正,二定,三相等”.
二、填空题:本大题共5小题,每小题5分,共25分
11.(5分)复数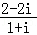 = ﹣2i .
= ﹣2i .
【考点】A5:复数的运算.菁优网版权所有
【专题】5N:数系的扩充和复数.
【分析】利用两个复数代数形式的乘除法法则化简所给的复数,可得结果.
【解答】解:复数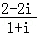 =
=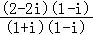 =
=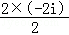 =﹣2i,
=﹣2i,
故答案为:﹣2i.
【点评】本题主要考查两个复数代数形式的乘除法法则的应用,属于基础题.
12.(5分)设f(x)是定义在R上的周期为2的函数,当x∈[﹣1,1)时,f(x)=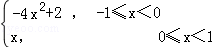 ,则f(
,则f(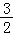 )= 1 .
)= 1 .
【考点】3Q:函数的周期性.菁优网版权所有
【专题】11:计算题.
【分析】由函数的周期性f(x+2)=f(x),将求f(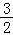 )的值转化成求f(
)的值转化成求f(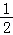 )的值.
)的值.
【解答】解:∵f(x)是定义在R上的周期为2的函数,
∴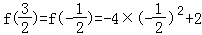 =1.
=1.
故答案为:1.
【点评】本题属于容易题,是考查函数周期性的简单考查,学生在计算时只要计算正确,往往都能把握住,在高考中,属于“送分题”.
13.(5分)如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为67°,30°,此时气球的高是46m,则河流的宽度BC约等于 60 m.(用四舍五入法将结果精确到个位.参考数据:sin67°≈0.92,cos67°≈0.39,sin37°≈0.60,cos37°≈0.80,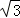 ≈1.73)
≈1.73)
【考点】HP:正弦定理;HR:余弦定理.菁优网版权所有
【专题】12:应用题;58:解三角形.
【分析】过A点作AD垂直于CB的延长线,垂足为D,分别在Rt△ACD、Rt△ABD中利用三角函数的定义,算出CD、BD的长,从而可得BC,即为河流在B、C两地的宽度.
【解答】解:过A点作AD垂直于CB的延长线,垂足为D,
则Rt△ACD中,∠C=30°,AD=46m,
AB=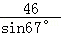 ,根据正弦定理,
,根据正弦定理, ,
,
得BC=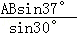 =
=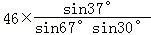 =60m.
=60m.
故答案为:60m.
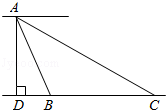
【点评】本题给出实际应用问题,求河流在B、C两地的宽度,着重考查了三角函数的定义、正余弦定理解三角形的知识,属于中档题.
14.(5分)设m∈R,过定点A的动直线x+my=0和过定点B的动直线mx﹣y﹣m+3=0交于点P(x,y).则|PA|•|PB|的最大值是 5 .
【考点】IT:点到直线的距离公式.菁优网版权所有
【专题】5B:直线与圆.
【分析】先计算出两条动直线经过的定点,即A和B,注意到两条动直线相互垂直的特点,则有PA⊥PB;再利用基本不等式放缩即可得出|PA|•|PB|的最大值.
【解答】解:由题意可知,动直线x+my=0经过定点A(0,0),
动直线mx﹣y﹣m+3=0即 m(x﹣1)﹣y+3=0,经过点定点B(1,3),
注意到动直线x+my=0和动直线mx﹣y﹣m+3=0始终垂直,P又是两条直线的交点,
则有PA⊥PB,∴|PA|2+|PB|2=|AB|2=10.
故|PA|•|PB|≤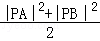 =5(当且仅当
=5(当且仅当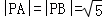 时取“=”)
时取“=”)
故答案为:5
【点评】本题是直线和不等式的综合考查,特别是“两条直线相互垂直”这一特征是本题解答的突破口,从而有|PA|2+|PB|2是个定值,再由基本不等式求解得出.直线位置关系和不等式相结合,不容易想到,是个灵活的好题.
15.(5分)以A表示值域为R的函数组成的集合,B表示具有如下性质的函数φ(x)组成的集合:对于函数φ(x),存在一个正数M,使得函数φ(x)的值域包含于区间[﹣M,M].例如,当φ1(x)=x3,φ2(x)=sinx时,φ1(x)∈A,φ2(x)∈B.现有如下命题:
①设函数f(x)的定义域为D,则“f(x)∈A”的充要条件是“∀b∈R,∃a∈D,f(a)=b”;
②函数f(x)∈B的充要条件是f(x)有最大值和最小值;
③若函数f(x),g(x)的定义域相同,且f(x)∈A,g(x)∈B,则f(x)+g(x)∉B.
④若函数f(x)=aln(x+2)+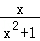 (x>﹣2,a∈R)有最大值,则f(x)∈B.
(x>﹣2,a∈R)有最大值,则f(x)∈B.
其中的真命题有 ①③④ .(写出所有真命题的序号)
【考点】29:充分条件、必要条件、充要条件;2H:全称量词和全称命题;2I:存在量词和特称命题;2K:命题的真假判断与应用;34:函数的值域.菁优网版权所有
【专题】23:新定义;3A:极限思想;51:函数的性质及应用;59:不等式的解法及应用;5L:简易逻辑.
【分析】根据题中的新定义,结合函数值域的概念,可判断出命题①②③是否正确,再利用导数研究命题④中函数的值域,可得到其真假情况,从而得到本题的结论.
【解答】解:(1)对于命题①,若对任意的b∈R,都∃a∈D使得f(a)=b,则f(x)的值域必为R.反之,f(x)的值域为R,则对任意的b∈R,都∃a∈D使得f(a)=b,故①是真命题;
(2)对于命题②,若函数f(x)∈B,即存在一个正数M,使得函数f(x)的值域包含于区间[﹣M,M].
∴﹣M≤f(x)≤M.例如:函数f(x)满足﹣2<f(x)<5,则有﹣5≤f(x)≤5,此时,f(x)无最大值,无最小值,故②是假命题;
(3)对于命题③,若函数f(x),g(x)的定义域相同,且f(x)∈A,g(x)∈B,则f(x)值域为R,f(x)∈(﹣∞,+∞),并且存在一个正数M,使得﹣M≤g(x)≤M.故f(x)+g(x)∈(﹣∞,+∞).
则f(x)+g(x)∉B,故③是真命题;
(4)对于命题④,∵﹣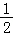 ≤
≤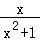 ≤
≤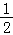 ,
,
当a>0或a<0时,aln(x+2)∈(﹣∞,+∞),f(x)均无最大值,若要使f(x)有最大值,则a=0,此时f(x)=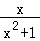 ,f(x)∈B,故④是真命题.
,f(x)∈B,故④是真命题.
故答案为①③④.
【点评】本题考查了函数值域的概念、基本不等式、充要条件,还考查了新定义概念的应用和极限思想.本题计算量较大,也有一定的思维难度,属于难题.
三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.
16.(12分)已知函数f(x)=sin(3x+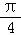 ).
).
(1)求f(x)的单调递增区间;
(2)若α是第二象限角,f(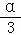 )=
)=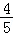 cos(α+
cos(α+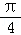 )cos2α,求cosα﹣sinα的值.
)cos2α,求cosα﹣sinα的值.
【考点】GP:两角和与差的三角函数;H5:正弦函数的单调性.菁优网版权所有
【专题】56:三角函数的求值.
【分析】(1)令 2kπ﹣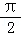 ≤3x+
≤3x+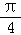 ≤2kπ+
≤2kπ+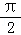 ,k∈z,求得x的范围,可得函数的增区间.
,k∈z,求得x的范围,可得函数的增区间.
(2)由函数的解析式可得 f(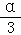 )=sin(α+
)=sin(α+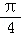 ),又f(
),又f(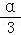 )=
)=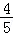 cos(α+
cos(α+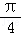 )cos2α,可得sin(α+
)cos2α,可得sin(α+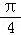 )=
)=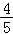 cos(α+
cos(α+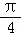 )cos2α,化简可得 (cosα﹣sinα)2=
)cos2α,化简可得 (cosα﹣sinα)2=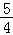 .再由α是第二象限角,cosα﹣sinα<0,从而求得cosα﹣sinα 的值.
.再由α是第二象限角,cosα﹣sinα<0,从而求得cosα﹣sinα 的值.
【解答】解:(1)∵函数f(x)=sin(3x+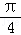 ),令 2kπ﹣
),令 2kπ﹣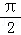 ≤3x+
≤3x+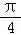 ≤2kπ+
≤2kπ+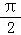 ,k∈Z,
,k∈Z,
求得 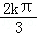 ﹣
﹣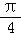 ≤x≤
≤x≤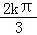 +
+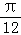 ,故函数的增区间为[
,故函数的增区间为[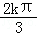 ﹣
﹣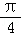 ,
,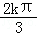 +
+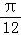 ],k∈Z.
],k∈Z.
(2)由函数的解析式可得 f(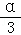 )=sin(α+
)=sin(α+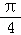 ),又f(
),又f(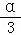 )=
)=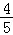 cos(α+
cos(α+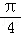 )cos2α,
)cos2α,
∴sin(α+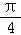 )=
)=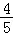 cos(α+
cos(α+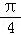 )cos2α,即sin(α+
)cos2α,即sin(α+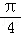 )=
)=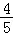 cos(α+
cos(α+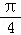 )(cos2α﹣sin2α),
)(cos2α﹣sin2α),
∴sinαcos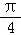 +cosαsin
+cosαsin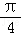 =
=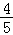 (cosαcos
(cosαcos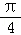 ﹣sinαsin
﹣sinαsin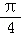 )(cosα﹣sinα)(cosα+sinα)
)(cosα﹣sinα)(cosα+sinα)
即 (sinα+cosα)=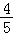 •(cosα﹣sinα)2(cosα+sinα),
•(cosα﹣sinα)2(cosα+sinα),
又∵α是第二象限角,∴cosα﹣sinα<0,
当sinα+cosα=0时,tanα=﹣1,sinα=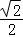 ,cosα=﹣
,cosα=﹣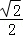 ,此时cosα﹣sinα=﹣
,此时cosα﹣sinα=﹣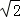 .
.
当sinα+cosα≠0时,此时cosα﹣sinα=﹣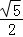 .
.
综上所述:cosα﹣sinα=﹣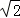 或﹣
或﹣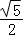 .
.
【点评】本题主要考查正弦函数的单调性,三角函数的恒等变换,体现了分类讨论的数学思想,属于中档题.
17.(12分)一款击鼓小游戏的规则如下:每盘游戏都需要击鼓三次,每次击鼓要么出现一次音乐,要么不出现音乐:每盘游戏击鼓三次后,出现一次音乐获得10分,出现两次音乐获得20分,出现三次音乐获得100分,没有出现音乐则扣除200分(即获得﹣200分).设每次击鼓出现音乐的概率为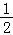 ,且各次击鼓出现音乐相互独立.
,且各次击鼓出现音乐相互独立.
(1)设每盘游戏获得的分数为X,求X的分布列;
(2)玩三盘游戏,至少有一盘出现音乐的概率是多少?
(3)玩过这款游戏的许多人都发现.若干盘游戏后,与最初分数相比,分数没有增加反而减少了.请运用概率统计的相关知识分析分数减少的原因.
【考点】CG:离散型随机变量及其分布列;CH:离散型随机变量的期望与方差.菁优网版权所有
【专题】5I:概率与统计.
【分析】(1)设每盘游戏获得的分数为X,求出对应的概率,即可求X的分布列;
(2)求出有一盘出现音乐的概率,独立重复试验的概率公式即可得到结论.
(3)计算出随机变量的期望,根据统计与概率的知识进行分析即可.
【解答】解:(1)X可能取值有﹣200,10,20,100.
则P(X=﹣200)=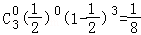 ,
,
P(X=10)=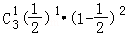 =
=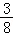
P(X=20)=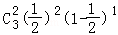 =
=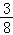 ,
,
P(X=100)=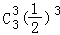 =
=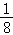 ,
,
故分布列为:
X | ﹣200 | 10 | 20 | 100 |
P |
|
|
| |
由(1)知,每盘游戏出现音乐的概率是p=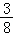 +
+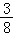
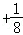 =
=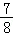 ,
,
则至少有一盘出现音乐的概率p=1﹣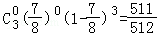 .
.
由(1)知,每盘游戏获得的分数为X的数学期望是E(X)=(﹣200)×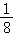 +10×
+10×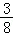 +20×
+20×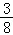
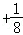 ×100=﹣
×100=﹣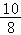 =
=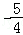 .
.
这说明每盘游戏平均得分是负分,由概率统计的相关知识可知:许多人经过若干盘游戏后,入最初的分数相比,分数没有增加反而会减少.
【点评】本题主要考查概率的计算,以及离散型分布列的计算,以及利用期望的计算,考查学生的计算能力.
18.(12分)三棱锥A﹣BCD及其侧视图、俯视图如图所示,设M,N分别为线段AD,AB的中点,P为线段BC上的点,且MN⊥NP.
(1)证明:P是线段BC的中点;
(2)求二面角A﹣NP﹣M的余弦值.
【考点】LS:直线与平面平行;MJ:二面角的平面角及求法.菁优网版权所有
【专题】5H:空间向量及应用.
【分析】(1)用线面垂直的性质和反证法推出结论,
(2)先建空间直角坐标系,再求平面的法向量,即可求出二面角A﹣NP﹣M的余弦值.
【解答】解:(1)由三棱锥A﹣BCD及其侧视图、俯视图可知,在三棱锥A﹣BCD中:
平面ABD⊥平面CBD,AB=AD=BD=CD=CB=2
设O为BD的中点,连接OA,OC
于是OA⊥BD,OC⊥BD 所以BD⊥平面OAC⇒BD⊥AC
因为M,N分别为线段AD,AB的中点,所以MN∥BD,MN⊥NP,故BD⊥NP
假设P不是线段BC的中点,则直线NP与直线AC是平面ABC内相交直线
从而BD⊥平面ABC,这与∠DBC=60°矛盾,所以P为线段BC的中点
(2)以O为坐标原点,OB,OC,OA分别为x,y,z轴建立空间直角坐标系,
则A(0,0,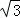 ),M(
),M(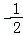 ,O,
,O,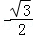 ),N(
),N(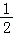 ,0,
,0,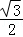 ),P(
),P(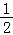 ,
,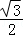 ,0)
,0)
于是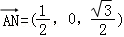 ,
,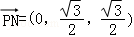 ,
,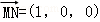
设平面ANP和平面NPM的法向量分别为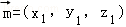 和
和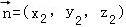
由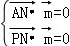 ,则
,则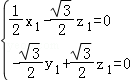 ,设z1=1,则
,设z1=1,则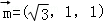
由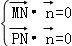 ,则
,则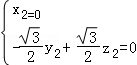 ,设z2=1,则
,设z2=1,则
cos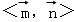 =
=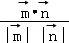 =
=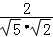 =
=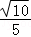
所以二面角A﹣NP﹣M的余弦值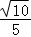
【点评】本题考查线线的位置关系,考查二面角知识的应用,解题的关键是掌握用向量的方法求二面角大小的步骤,属于中档题.
19.(12分)设等差数列{an}的公差为d,点(an,bn)在函数f(x)=2x的图象上(n∈N*).
(1)若a1=﹣2,点(a8,4b7)在函数f(x)的图象上,求数列{an}的前n项和Sn;
(2)若a1=1,函数f(x)的图象在点(a2,b2)处的切线在x轴上的截距为2﹣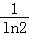 ,求数列{
,求数列{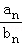 }的前n项和Tn.
}的前n项和Tn.
【考点】8E:数列的求和;8I:数列与函数的综合.菁优网版权所有
【专题】51:函数的性质及应用;54:等差数列与等比数列.
【分析】(1)由于点(an,bn)在函数f(x)=2x的图象上,可得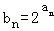 ,又等差数列{an}的公差为d,利用等差数列的通项公式可得
,又等差数列{an}的公差为d,利用等差数列的通项公式可得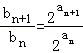 =2d.由于点
=2d.由于点
(a8,4b7)在函数f(x)的图象上,可得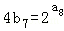 =b8,进而得到
=b8,进而得到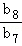 =4=2d,解得d.再利用等差数列的前n项和公式即可得出.
=4=2d,解得d.再利用等差数列的前n项和公式即可得出.
(2)利用导数的几何意义可得函数f(x)的图象在点(a2,b2)处的切线方程,即可解得a2.进而得到an,bn.再利用“错位相减法”即可得出.
【解答】解:(1)∵点(an,bn)在函数f(x)=2x的图象上,
∴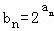 ,
,
又等差数列{an}的公差为d,
∴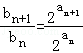 =
=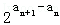 =2d,
=2d,
∵点(a8,4b7)在函数f(x)的图象上,
∴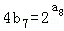 =b8,
=b8,
∴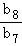 =4=2d,解得d=2.
=4=2d,解得d=2.
又a1=﹣2,∴Sn=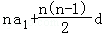 =﹣2n+
=﹣2n+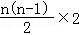 =n2﹣3n.
=n2﹣3n.
(2)由f(x)=2x,∴f′(x)=2xln2,
∴函数f(x)的图象在点(a2,b2)处的切线方程为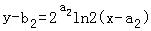 ,
,
又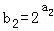 ,令y=0可得x=
,令y=0可得x=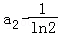 ,
,
∴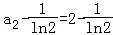 ,解得a2=2.
,解得a2=2.
∴d=a2﹣a1=2﹣1=1.
∴an=a1+(n﹣1)d=1+(n﹣1)×1=n,
∴bn=2n.
∴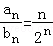 .
.
∴Tn=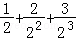 +…+
+…+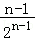 +
+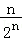 ,
,
∴2Tn=1+ +
+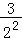 +…+
+…+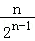 ,
,
两式相减得Tn=1+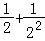 +…+
+…+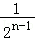 ﹣
﹣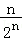 =
=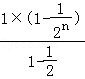 ﹣
﹣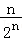
=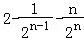
=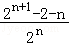 .
.
【点评】本题综合考查了指数函数的运算性质、导数的几何意义、等差数列与等比数列的通项公式及其前n项和公式等基础知识与基本技能方法,考查了推理能力、计算能力、“错位相减法”,属于难题.
20.(13分)已知椭圆C: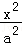 +
+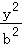 =1(a>b>0)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
=1(a>b>0)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(1)求椭圆C的标准方程;
(2)设F为椭圆C的左焦点,T为直线x=﹣3上任意一点,过F作TF的垂线交椭圆C于点P,Q.
①证明:OT平分线段PQ(其中O为坐标原点);
②当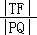 最小时,求点T的坐标.
最小时,求点T的坐标.
【考点】K3:椭圆的标准方程;KH:直线与圆锥曲线的综合.菁优网版权所有
【专题】5E:圆锥曲线中的最值与范围问题.
【分析】第(1)问中,由正三角形底边与高的关系,a2=b2+c2及焦距2c=4建立方程组求得a2,b2;
第(2)问中,先设点的坐标及直线PQ的方程,利用两点间距离公式及弦长公式将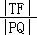 表示出来,由
表示出来,由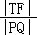 取最小值时的条件获得等量关系,从而确定点T的坐标.
取最小值时的条件获得等量关系,从而确定点T的坐标.
【解答】解:(1)依题意有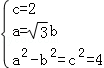 解得
解得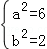
所以椭圆C的标准方程为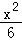 +
+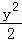 =1.
=1.
(2)设T(﹣3,t),P(x1,y1),Q(x2,y2),PQ的中点为N(x0,y0),
①证明:由F(﹣2,0),可设直线PQ的方程为x=my﹣2,则PQ的斜率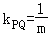 .
.
由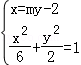 ⇒(m2+3)y2﹣4my﹣2=0,
⇒(m2+3)y2﹣4my﹣2=0,
所以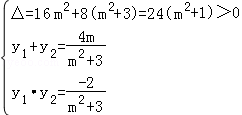 ,
,
于是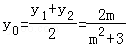 ,从而
,从而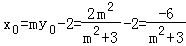 ,
,
即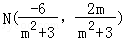 ,则直线ON的斜率
,则直线ON的斜率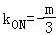 ,
,
又由PQ⊥TF知,直线TF的斜率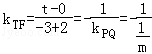 ,得t=m.
,得t=m.
从而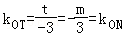 ,即kOT=kON,
,即kOT=kON,
所以O,N,T三点共线,从而OT平分线段PQ,故得证.
②由两点间距离公式得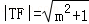 ,
,
由弦长公式得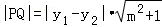 =
=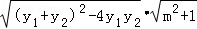 =
=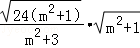 ,
,
所以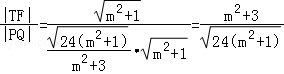 ,
,
令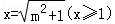 ,则
,则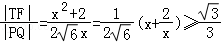 (当且仅当x2=2时,取“=”号),
(当且仅当x2=2时,取“=”号),
所以当 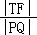 最小时,由x2=2=m2+1,得m=1或m=﹣1,此时点T的坐标为(﹣3,1)或(﹣3,﹣1).
最小时,由x2=2=m2+1,得m=1或m=﹣1,此时点T的坐标为(﹣3,1)或(﹣3,﹣1).
【点评】本题属相交弦问题,应注意考虑这几个方面:
1、设交点坐标,设直线方程;
2、联立直线与椭圆方程,消去y或x,得到一个关于x或y一元二次方程,利用韦达定理;
3、利用基本不等式或函数的单调性探求最值问题.
21.(14分)已知函数f(x)=ex﹣ax2﹣bx﹣1,其中a,b∈R,e=2.71828…为自然对数的底数.
(1)设g(x)是函数f(x)的导函数,求函数g(x)在区间[0,1]上的最小值;
(2)若f(1)=0,函数f(x)在区间(0,1)内有零点,求a的取值范围.
【考点】51:函数的零点;6E:利用导数研究函数的最值.菁优网版权所有
【专题】53:导数的综合应用.
【分析】(1)求出f(x)的导数得g(x),再求出g(x)的导数,对它进行讨论,从而判断g(x)的单调性,求出g(x)的最小值;
(2)利用等价转换,若函数f(x)在区间(0,1)内有零点,则函数f(x)在区间(0,1)内至少有三个单调区间,所以g(x)在(0,1)上应有两个不同的零点.
【解答】解:∵f(x)=ex﹣ax2﹣bx﹣1,∴g(x)=f′(x)=ex﹣2ax﹣b,
又g′(x)=ex﹣2a,x∈[0,1],∴1≤ex≤e,
∴①当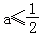 时,则2a≤1,g′(x)=ex﹣2a≥0,
时,则2a≤1,g′(x)=ex﹣2a≥0,
∴函数g(x)在区间[0,1]上单调递增,g(x)min=g(0)=1﹣b;
②当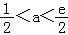 ,则1<2a<e,
,则1<2a<e,
∴当0<x<ln(2a)时,g′(x)=ex﹣2a<0,当ln(2a)<x<1时,g′(x)=ex﹣2a>0,
∴函数g(x)在区间[0,ln(2a)]上单调递减,在区间[ln(2a),1]上单调递增,
g(x)min=g[ln(2a)]=2a﹣2aln(2a)﹣b;
③当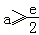 时,则2a≥e,g′(x)=ex﹣2a≤0,
时,则2a≥e,g′(x)=ex﹣2a≤0,
∴函数g(x)在区间[0,1]上单调递减,g(x)min=g(1)=e﹣2a﹣b,
综上:函数g(x)在区间[0,1]上的最小值为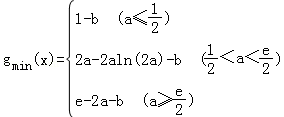 ;
;
(2)由f(1)=0,⇒e﹣a﹣b﹣1=0⇒b=e﹣a﹣1,又f(0)=0,
若函数f(x)在区间(0,1)内有零点,则函数f(x)在区间(0,1)内至少有三个单调区间,
由(1)知当a≤ 或a≥
或a≥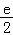 时,函数g(x)在区间[0,1]上单调,不可能满足“函数f(x)在区间(0,1)内至少有三个单调区间”这一要求.
时,函数g(x)在区间[0,1]上单调,不可能满足“函数f(x)在区间(0,1)内至少有三个单调区间”这一要求.
若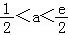 ,则gmin(x)=2a﹣2aln(2a)﹣b=3a﹣2aln(2a)﹣e+1
,则gmin(x)=2a﹣2aln(2a)﹣b=3a﹣2aln(2a)﹣e+1
令h(x)= (1<x<e)
(1<x<e)
则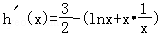 =
=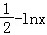 ,∴
,∴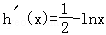 .由
.由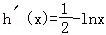 >0⇒x<
>0⇒x<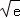
∴h(x)在区间(1,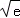 )上单调递增,在区间(
)上单调递增,在区间(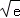 ,e)上单调递减,
,e)上单调递减,
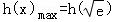 =
=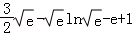 =
=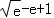 <0,即gmin(x)<0 恒成立,
<0,即gmin(x)<0 恒成立,
∴函数f(x)在区间(0,1)内至少有三个单调区间⇔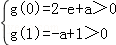 ⇒
⇒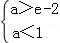 ,
,
又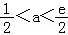 ,所以e﹣2<a<1,
,所以e﹣2<a<1,
综上得:e﹣2<a<1.
另解:由g(0)>0,g(1)>0 解出e﹣2<a<1,
再证明此时f(x)min<0 由于f(x)最小时,f'(x)=g(x)=ex﹣2ax﹣b=0,
故有ex=2ax+b且f(1)=0知e﹣1=a+b,
则f(x)min=2ax+b﹣ax2﹣(e﹣1﹣a)x﹣1=﹣ax2+(3a+1﹣e)x+e﹣a﹣2,
开口向下,最大值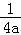 (5a2﹣(2e+2)a+e2﹣2e),分母为正,
(5a2﹣(2e+2)a+e2﹣2e),分母为正,
只需看分子正负,分子<5﹣(2e+2)+e2﹣2e(a=1时取最大)=e2﹣4e+3<0,
故f(x)min<0,
故 e﹣2<a<1.
【点评】本题考查了,利用导数求函数的单调区间,分类讨论思想,等价转换思想,函数的零点等知识点.是一道导数的综合题,难度较大.