2015年四川省高考数学试卷(理科)(含解析版)

2015年四川省高考数学试卷(理科)
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一个是符合题目要求的。
1.(5分)设集合A={x|(x+1)(x﹣2)<0},集合B={x|1<x<3},则A∪B=( )
A.{x|﹣1<x<3}B.{x|﹣1<x<1} C.{x|1<x<2} D.{x|2<x<3}
2.(5分)设i是虚数单位,则复数i3﹣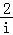 =( )
=( )
A.﹣iB.﹣3i C.i D.3i
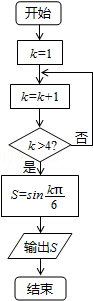
3.(5分)执行如图所示的程序框图,输出s的值为( )
A.﹣B.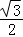 C.﹣
C.﹣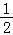 D.
D.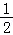
4.(5分)下列函数中,最小正周期为π且图象关于原点对称的函数是( )
A.y=cos(2x+)B.y=sin(2x+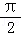 )
)
C.y=sin2x+cos2xD.y=sinx+cosx
5.(5分)过双曲线x2﹣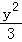 =1的右焦点且与x轴垂直的直线,交该双曲线的两条渐近线于A、B两点,则|AB|=( )
=1的右焦点且与x轴垂直的直线,交该双曲线的两条渐近线于A、B两点,则|AB|=( )
A.B.2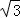 C.6 D.4
C.6 D.4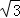
6.(5分)用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40000大的偶数共有( )
A.144个B.120个 C.96个 D.72个
7.(5分)设四边形ABCD为平行四边形,|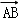 |=6,|
|=6,|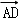 |=4,若点M、N满足
|=4,若点M、N满足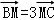 ,
,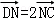 ,则
,则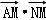 =( )
=( )
A.20B.15 C.9 D.6
8.(5分)设a、b都是不等于1的正数,则“3a>3b>3”是“loga3<logb3”的( )
A.充要条件B.充分不必要条件
C.必要不充分条件D.既不充分也不必要条件
9.(5分)如果函数f(x)=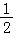 (m﹣2)x2+(n﹣8)x+1(m≥0,n≥0)在区间[
(m﹣2)x2+(n﹣8)x+1(m≥0,n≥0)在区间[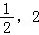 ]上单调递减,那么mn的最大值为( )
]上单调递减,那么mn的最大值为( )
A.16B.18 C.25 D.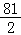
10.(5分)设直线l与抛物线y2=4x相交于A、B两点,与圆(x﹣5)2+y2=r2(r>0)相切于点M,且M为线段AB的中点,若这样的直线l恰有4条,则r的取值范围是( )
A.(1,3)B.(1,4) C.(2,3) D.(2,4)
二、填空题:本大题共5小题,每小题5分,共25分。
11.(5分)在(2x﹣1)5的展开式中,含x2的项的系数是 (用数字填写答案).
12.(5分)sin15°+sin75°的值是 .
13.(5分)某食品的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系y=ekx+b(e=2.718…为自然对数的底数,k、b为常数).若该食品在0℃的保鲜时间是192小时,在22℃的保鲜时间是48小时,则该食品在33℃的保鲜时间是 小时.
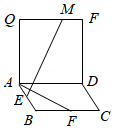
14.(5分)如图,四边形ABCD和ADPQ均为正方形,他们所在的平面互相垂直,动点M在线段PQ上,E、F分别为AB、BC的中点,设异面直线EM与AF所成的角为θ,则cosθ的最大值为 .
15.(5分)已知函数f(x)=2x,g(x)=x2+ax(其中a∈R).对于不相等的实数x1、x2,设m=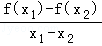 ,n=
,n=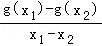 .现有如下命题:
.现有如下命题:
①对于任意不相等的实数x1、x2,都有m>0;
②对于任意的a及任意不相等的实数x1、x2,都有n>0;
③对于任意的a,存在不相等的实数x1、x2,使得m=n;
④对于任意的a,存在不相等的实数x1、x2,使得m=﹣n.
其中的真命题有 (写出所有真命题的序号).
三、解答题:本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤。
16.(12分)设数列{an}(n=1,2,3,…)的前n项和Sn满足Sn=2an﹣a1,且a1,a2+1,a3成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)记数列{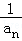 }的前n项和为Tn,求使得|Tn﹣1|
}的前n项和为Tn,求使得|Tn﹣1|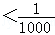 成立的n的最小值.
成立的n的最小值.
17.(12分)某市A、B两所中学的学生组队参加辩论赛,A中学推荐了3名男生、2名女生,B中学推荐了3名男生、4名女生,两校所推荐的学生一起参加集训.由于集训后队员水平相当,从参加集训的男生中随机抽取3人,女生中随机抽取3人组成代表队.
(Ⅰ)求A中学至少有1名学生入选代表队的概率;
(Ⅱ)某场比赛前,从代表队的6名队员中随机抽取4人参赛,设X表示参赛的男生人数,求X的分布列和数学期望.
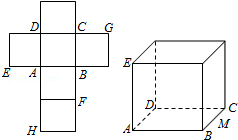
18.(12分)一个正方体的平面展开图及该正方体的直观图的示意图如图所示.在正方体中,设BC的中点为M、GH的中点为N.
(Ⅰ)请将字母F、G、H标记在正方体相应的顶点处(不需说明理由);
(Ⅱ)证明:直线MN∥平面BDH;
(Ⅲ)求二面角A﹣EG﹣M的余弦值.
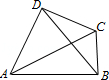
19.(12分)如图,A、B、C、D为平面四边形ABCD的四个内角.
(Ⅰ)证明:tan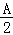 =
=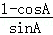 ;
;
(Ⅱ)若A+C=180°,AB=6,BC=3,CD=4,AD=5,求tan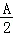 +tan
+tan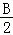 +tan
+tan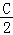 +tan
+tan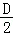 的值.
的值.
20.(13分)如图,椭圆E: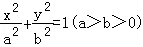 的离心率是
的离心率是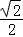 ,过点P(0,1)的动直线l与椭圆相交于A、B两点,当直线l平行于x轴时,直线l被椭圆E截得的线段长为2
,过点P(0,1)的动直线l与椭圆相交于A、B两点,当直线l平行于x轴时,直线l被椭圆E截得的线段长为2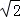 .
.
(Ⅰ)求椭圆E的方程;
(Ⅱ)在平面直角坐标系xOy中,是否存在与点P不同的定点Q,使得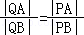 恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
21.(14分)已知函数f(x)=﹣2(x+a)lnx+x2﹣2ax﹣2a2+a,其中a>0.
(Ⅰ)设g(x)是f(x)的导函数,讨论g(x)的单调性;
(Ⅱ)证明:存在a∈(0,1),使得f(x)≥0在区间(1,+∞)内恒成立,且f(x)=0在区间(1,+∞)内有唯一解.
2015年四川省高考数学试卷(理科)
参考答案与试题解析
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一个是符合题目要求的。
1.(5分)设集合A={x|(x+1)(x﹣2)<0},集合B={x|1<x<3},则A∪B=( )
A.{x|﹣1<x<3}B.{x|﹣1<x<1} C.{x|1<x<2} D.{x|2<x<3}
【考点】1D:并集及其运算.菁优网版权所有
【专题】51:函数的性质及应用.
【分析】求解不等式得出集合A={x|﹣1<x<2},
根据集合的并集可求解答案.
【解答】解:∵集合A={x|(x+1)(x﹣2)<0},集合B={x|1<x<3},
∴集合A={x|﹣1<x<2},
∵A∪B={x|﹣1<x<3},
故选:A.
【点评】本题考查了二次不等式的求解,集合的运算,属于容易题.
2.(5分)设i是虚数单位,则复数i3﹣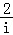 =( )
=( )
A.﹣iB.﹣3i C.i D.3i
【考点】A5:复数的运算.菁优网版权所有
【专题】11:计算题.
【分析】通分得出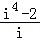 ,利用i的性质运算即可.
,利用i的性质运算即可.
【解答】解:∵i是虚数单位,则复数i3﹣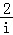 ,
,
∴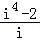 =
=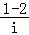 =
=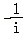 =i,
=i,
故选:C.
【点评】本题考查了复数的运算,掌握好运算法则即可,属于计算题.
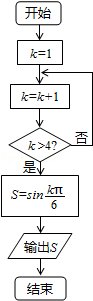
3.(5分)执行如图所示的程序框图,输出s的值为( )
A.﹣B.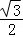 C.﹣
C.﹣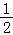 D.
D.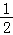
【考点】EF:程序框图.菁优网版权所有
【专题】27:图表型;5K:算法和程序框图.
【分析】模拟执行程序框图,依次写出每次循环得到的k的值,当k=5时满足条件k>4,计算并输出S的值为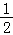 .
.
【解答】解:模拟执行程序框图,可得
k=1
k=2
不满足条件k>4,k=3
不满足条件k>4,k=4
不满足条件k>4,k=5
满足条件k>4,S=sin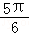 =
=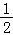 ,
,
输出S的值为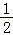 .
.
故选:D.
【点评】本题主要考查了循环结构的程序框图,属于基础题.
4.(5分)下列函数中,最小正周期为π且图象关于原点对称的函数是( )
A.y=cos(2x+)B.y=sin(2x+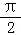 )
)
C.y=sin2x+cos2xD.y=sinx+cosx
【考点】GP:两角和与差的三角函数;H1:三角函数的周期性.菁优网版权所有
【专题】57:三角函数的图像与性质.
【分析】求出函数的周期,函数的奇偶性,判断求解即可.
【解答】解:
y=cos(2x+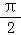 )=﹣sin2x,是奇函数,函数的周期为:π,满足题意,所以A正确
)=﹣sin2x,是奇函数,函数的周期为:π,满足题意,所以A正确
y=sin(2x+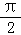 )=cos2x,函数是偶函数,周期为:π,不满足题意,所以B不正确;
)=cos2x,函数是偶函数,周期为:π,不满足题意,所以B不正确;
y=sin2x+cos2x=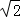 sin(2x+
sin(2x+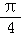 ),函数是非奇非偶函数,周期为π,所以C不正确;
),函数是非奇非偶函数,周期为π,所以C不正确;
y=sinx+cosx=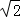 sin(x+
sin(x+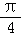 ),函数是非奇非偶函数,周期为2π,所以D不正确;
),函数是非奇非偶函数,周期为2π,所以D不正确;
故选:A.
【点评】本题考查两角和与差的三角函数,函数的奇偶性以及红丝带周期的求法,考查计算能力.
5.(5分)过双曲线x2﹣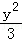 =1的右焦点且与x轴垂直的直线,交该双曲线的两条渐近线于A、B两点,则|AB|=( )
=1的右焦点且与x轴垂直的直线,交该双曲线的两条渐近线于A、B两点,则|AB|=( )
A.B.2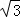 C.6 D.4
C.6 D.4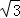
【考点】KC:双曲线的性质.菁优网版权所有
【专题】5D:圆锥曲线的定义、性质与方程.
【分析】求出双曲线的渐近线方程,求出AB的方程,得到AB坐标,即可求解|AB|.
【解答】解:双曲线x2﹣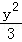 =1的右焦点(2,0),渐近线方程为y=
=1的右焦点(2,0),渐近线方程为y=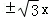 ,
,
过双曲线x2﹣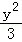 =1的右焦点且与x轴垂直的直线,x=2,
=1的右焦点且与x轴垂直的直线,x=2,
可得yA=2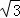 ,yB=﹣2
,yB=﹣2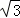 ,
,
∴|AB|=4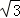 .
.
故选:D.
【点评】本题考查双曲线的简单性质的应用,考查基本知识的应用.
6.(5分)用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40000大的偶数共有( )
A.144个B.120个 C.96个 D.72个
【考点】D9:排列、组合及简单计数问题.菁优网版权所有
【专题】12:应用题;5O:排列组合.
【分析】根据题意,符合条件的五位数首位数字必须是4、5其中1个,末位数字为0、2、4中其中1个;进而对首位数字分2种情况讨论,①首位数字为5时,②首位数字为4时,每种情况下分析首位、末位数字的情况,再安排剩余的三个位置,由分步计数原理可得其情况数目,进而由分类加法原理,计算可得答案.
【解答】解:根据题意,符合条件的五位数首位数字必须是4、5其中1个,末位数字为0、2、4中其中1个;
分两种情况讨论:
①首位数字为5时,末位数字有3种情况,在剩余的4个数中任取3个,放在剩余的3个位置上,有A43=24种情况,此时有3×24=72个,
②首位数字为4时,末位数字有2种情况,在剩余的4个数中任取3个,放在剩余的3个位置上,有A43=24种情况,此时有2×24=48个,
共有72+48=120个.
故选:B.
【点评】本题考查计数原理的运用,关键是根据题意,分析出满足题意的五位数的首位、末位数字的特征,进而可得其可选的情况.
7.(5分)设四边形ABCD为平行四边形,|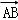 |=6,|
|=6,|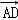 |=4,若点M、N满足
|=4,若点M、N满足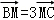 ,
,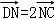 ,则
,则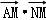 =( )
=( )
A.20B.15 C.9 D.6
【考点】9O:平面向量数量积的性质及其运算.菁优网版权所有
【专题】5A:平面向量及应用.
【分析】根据图形得出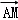 =
=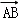 +
+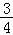
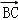 =
=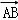
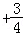
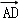 ,
,
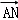 =
=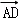
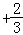
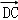 =
=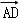
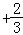
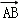 ,
,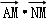 =
=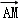 •(
•(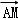
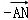 )=
)=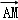 2﹣
2﹣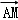
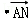 ,
,
结合向量结合向量的数量积求解即可.
【解答】解:∵四边形ABCD为平行四边形,点M、N满足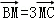 ,
,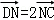 ,
,
∴根据图形可得: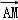 =
=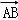 +
+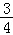
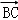 =
=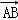
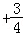
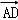 ,
,
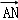 =
=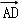
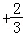
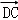 =
=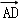
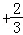
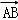 ,
,
∴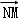 =
=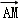
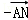 ,
,
∵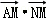 =
=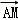 •(
•(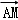
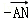 )=
)=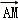 2﹣
2﹣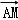
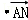 ,
,
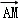 2=
2=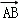 2
2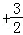
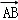
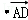
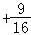
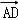 2,
2,
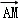
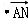 =
=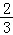
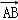 2
2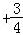
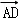 2
2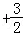
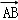
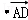 ,
,
|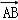 |=6,|
|=6,|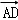 |=4,
|=4,
∴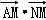 =
= 2
2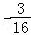
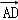 2=12﹣3=9
2=12﹣3=9
故选:C.
【点评】本题考查了平面向量的运算,数量积的运用,考查了数形结合的思想,关键是向量的分解,表示.
8.(5分)设a、b都是不等于1的正数,则“3a>3b>3”是“loga3<logb3”的( )
A.充要条件B.充分不必要条件
C.必要不充分条件D.既不充分也不必要条件
【考点】29:充分条件、必要条件、充要条件.菁优网版权所有
【专题】5L:简易逻辑.
【分析】求解3a>3b>3,得出a>b>1,
loga3<logb3,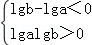 或
或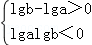 根据对数函数的性质求解即可,
根据对数函数的性质求解即可,
再利用充分必要条件的定义判断即可.
【解答】解:a、b都是不等于1的正数,
∵3a>3b>3,
∴a>b>1,
∵loga3<logb3,
∴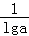
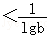 ,
,
即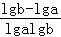 <0,
<0,
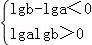 或
或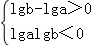
求解得出:a>b>1或1>a>b>0或b>1,0<a<1
根据充分必要条件定义得出:“3a>3b>3”是“loga3<logb3”的充分条不必要件,
故选:B.
【点评】本题综合考查了指数,对数函数的单调性,充分必要条件的定义,属于综合题目,关键是分类讨论.
9.(5分)如果函数f(x)=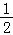 (m﹣2)x2+(n﹣8)x+1(m≥0,n≥0)在区间[
(m﹣2)x2+(n﹣8)x+1(m≥0,n≥0)在区间[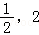 ]上单调递减,那么mn的最大值为( )
]上单调递减,那么mn的最大值为( )
A.16B.18 C.25 D.
【考点】3V:二次函数的性质与图象;6D:利用导数研究函数的极值;7F:基本不等式及其应用.菁优网版权所有
【专题】51:函数的性质及应用;52:导数的概念及应用;59:不等式的解法及应用.
【分析】函数f(x)=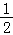 (m﹣2)x2+(n﹣8)x+1(m≥0,n≥0)在区间[
(m﹣2)x2+(n﹣8)x+1(m≥0,n≥0)在区间[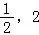 ]上单调递减,则f′(x)≤0,故(m﹣2)x+n﹣8≤0在[
]上单调递减,则f′(x)≤0,故(m﹣2)x+n﹣8≤0在[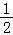 ,2]上恒成立.而(m﹣2)x+n﹣8是一次函数,在[
,2]上恒成立.而(m﹣2)x+n﹣8是一次函数,在[ ,2]上的图象是一条线段.故只须在两个端点处f′(
,2]上的图象是一条线段.故只须在两个端点处f′( )≤0,f′(2)≤0即可.结合基本不等式求出mn的最大值.
)≤0,f′(2)≤0即可.结合基本不等式求出mn的最大值.
【解答】解:∵函数f(x)= (m﹣2)x2+(n﹣8)x+1(m≥0,n≥0)在区间[
(m﹣2)x2+(n﹣8)x+1(m≥0,n≥0)在区间[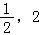 ]上单调递减,
]上单调递减,
∴f′(x)≤0,故(m﹣2)x+n﹣8≤0在[ ,2]上恒成立.而(m﹣2)x+n﹣8是一次函数,在[
,2]上恒成立.而(m﹣2)x+n﹣8是一次函数,在[ ,2]上的图象是一条线段.故只须在两个端点处f′(
,2]上的图象是一条线段.故只须在两个端点处f′( )≤0,f′(2)≤0即可.即
)≤0,f′(2)≤0即可.即
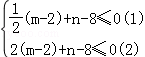
由(2)得m≤ (12﹣n),
(12﹣n),
∴mn≤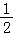 n(12﹣n)≤
n(12﹣n)≤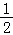
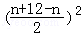 =18,当且仅当m=3,n=6时取得最大值,经检验m=3,n=6满足(1)和(2).
=18,当且仅当m=3,n=6时取得最大值,经检验m=3,n=6满足(1)和(2).
故选:B.
解法二:
∵函数f(x)=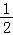 (m﹣2)x2+(n﹣8)x+1(m≥0,n≥0)在区间[
(m﹣2)x2+(n﹣8)x+1(m≥0,n≥0)在区间[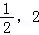 ]上单调递减,
]上单调递减,
∴①m=2,n<8
对称轴x=﹣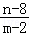 ,
,
②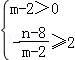 即
即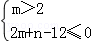
③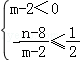 即
即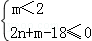
设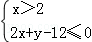 或
或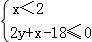 或
或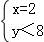
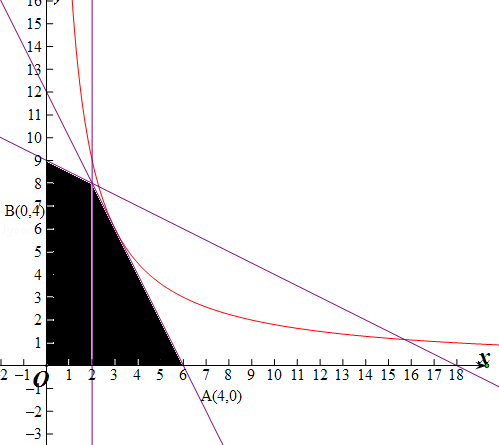
设y=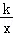 ,y′=
,y′=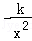 ,
,
当切点为(x0,y0),k取最大值.
①﹣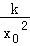 =﹣2.k=2x
=﹣2.k=2x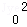 ,
,
∴y0=﹣2x0+12,y0=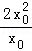 =2x0,可得x0=3,y0=6,
=2x0,可得x0=3,y0=6,
∵x=3>2
∴k的最大值为3×6=18
②﹣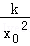 =﹣
=﹣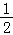 .,k=
.,k=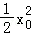 ,
,
y0=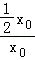 =
=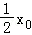 ,
,
2y0+x0﹣18=0,
解得:x0=9,y0=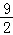
∵x0<2
∴不符合题意.
③m=2,n=8,k=mn=16
综合得出:m=3,n=6时k最大值k=mn=18,
故选:B.
【点评】本题综合考查了函数方程的运用,线性规划问题,结合导数的概念,运用几何图形判断,难度较大,属于难题.
10.(5分)设直线l与抛物线y2=4x相交于A、B两点,与圆(x﹣5)2+y2=r2(r>0)相切于点M,且M为线段AB的中点,若这样的直线l恰有4条,则r的取值范围是( )
A.(1,3)B.(1,4) C.(2,3) D.(2,4)
【考点】J9:直线与圆的位置关系;K8:抛物线的性质.菁优网版权所有
【专题】15:综合题;2:创新题型;26:开放型;5B:直线与圆;5D:圆锥曲线的定义、性质与方程.
【分析】先确定M的轨迹是直线x=3,代入抛物线方程可得y=±2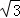 ,所以交点与圆心(5,0)的距离为4,即可得出结论.
,所以交点与圆心(5,0)的距离为4,即可得出结论.
【解答】解:设A(x1,y1),B(x2,y2),M(x0,y0),
斜率存在时,设斜率为k,则y12=4x1,y22=4x2,
则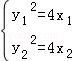 ,相减,得(y1+y2)(y1﹣y2)=4(x1﹣x2),
,相减,得(y1+y2)(y1﹣y2)=4(x1﹣x2),
当l的斜率存在时,利用点差法可得ky0=2,
因为直线与圆相切,所以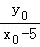 =﹣
=﹣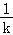 ,所以x0=3,
,所以x0=3,
即M的轨迹是直线x=3.
将x=3代入y2=4x,得y2=12,∴﹣2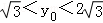 ,
,
∵M在圆上,∴(x0﹣5)2+y02=r2,∴r2=y02+4<12+4=16,
∵直线l恰有4条,∴y0≠0,∴4<r2<16,
故2<r<4时,直线l有2条;
斜率不存在时,直线l有2条;
所以直线l恰有4条,2<r<4,
故选:D.
【点评】本题考查直线与抛物线、圆的位置关系,考查点差法,考查学生分析解决问题的能力,属于中档题.
二、填空题:本大题共5小题,每小题5分,共25分。
11.(5分)在(2x﹣1)5的展开式中,含x2的项的系数是 ﹣40 (用数字填写答案).
【考点】DA:二项式定理.菁优网版权所有
【专题】5P:二项式定理.
【分析】根据所给的二项式,利用二项展开式的通项公式写出第r+1项,整理成最简形式,令x的指数为2求得r,再代入系数求出结果.
【解答】解:根据所给的二项式写出展开式的通项,
Tr+1=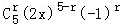 ;
;
要求x2的项的系数,
∴5﹣r=2,
∴r=3,
∴x2的项的系数是22(﹣1)3C53=﹣40.
故答案为:﹣40.
【点评】本题考查二项式定理的应用,本题解题的关键是正确写出二项展开式的通项,在这种题目中通项是解决二项展开式的特定项问题的工具.
12.(5分)sin15°+sin75°的值是 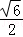 .
.
【考点】GF:三角函数的恒等变换及化简求值;GP:两角和与差的三角函数.菁优网版权所有
【专题】56:三角函数的求值.
【分析】利用诱导公式以及两角和的正弦函数化简求解即可.
【解答】解:sin15°+sin75°=sin15°+cos15°=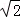 (sin15°cos45°+cos15°sin45°)=
(sin15°cos45°+cos15°sin45°)=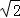 sin60°=
sin60°=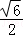 .
.
故答案为: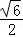 .
.
【点评】本题考查两角和的正弦函数,三角函数的化简求值,考查计算能力.
13.(5分)某食品的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系y=ekx+b(e=2.718…为自然对数的底数,k、b为常数).若该食品在0℃的保鲜时间是192小时,在22℃的保鲜时间是48小时,则该食品在33℃的保鲜时间是 24 小时.
【考点】57:函数与方程的综合运用.菁优网版权所有
【专题】11:计算题;51:函数的性质及应用.
【分析】由题意可得,x=0时,y=192;x=22时,y=48.代入函数y=ekx+b,解方程,可得k,b,再由x=33,代入即可得到结论.
【解答】解:由题意可得,x=0时,y=192;x=22时,y=48.
代入函数y=ekx+b,
可得eb=192,e22k+b=48,
即有e11k= ,eb=192,
,eb=192,
则当x=33时,y=e33k+b= ×192=24.
×192=24.
故答案为:24.
【点评】本题考查函数的解析式的求法和运用,考查运算能力,属于中档题.
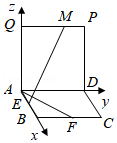
14.(5分)如图,四边形ABCD和ADPQ均为正方形,他们所在的平面互相垂直,动点M在线段PQ上,E、F分别为AB、BC的中点,设异面直线EM与AF所成的角为θ,则cosθ的最大值为 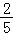 .
.
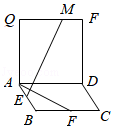
【考点】LM:异面直线及其所成的角.菁优网版权所有
【专题】5G:空间角;5H:空间向量及应用.
【分析】首先以AB,AD,AQ三直线为x,y,z轴,建立空间直角坐标系,并设正方形边长为2,M(0,y,2),从而可求出向量 的坐标,由cosθ=
的坐标,由cosθ=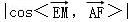 得到
得到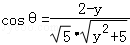 ,对函数
,对函数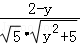 求导,根据导数符号即可判断该函数为减函数,从而求出cosθ的最大值.
求导,根据导数符号即可判断该函数为减函数,从而求出cosθ的最大值.
【解答】解:根据已知条件,AB,AD,AQ三直线两两垂直,分别以这三直线为x,y,z轴,建立如图所示空间直角坐标系,设AB=2,则:
A(0,0,0),E(1,0,0),F(2,1,0);
M在线段PQ上,设M(0,y,2),0≤y≤2;
∴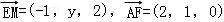 ;
;
∴cosθ=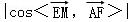 =
=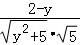 ;
;
设f(y)=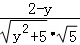 ,
,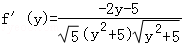 ;
;
函数g(y)=﹣2y﹣5是一次函数,且为减函数,g(0)=﹣5<0;
∴g(y)<0在[0,2]恒成立,∴f′(y)<0;
∴f(y)在[0,2]上单调递减;
∴y=0时,f(y)取到最大值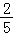 .
.
故答案为: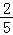 .
.
【点评】考查建立空间直角坐标系,利用空间向量解决异面直线所成角的问题,异面直线所成角的概念及其范围,向量夹角的概念及其范围,以及向量夹角余弦的坐标公式,函数导数符号和函数单调性的关系.
15.(5分)已知函数f(x)=2x,g(x)=x2+ax(其中a∈R).对于不相等的实数x1、x2,设m=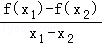 ,n=
,n=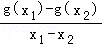 .现有如下命题:
.现有如下命题:
①对于任意不相等的实数x1、x2,都有m>0;
②对于任意的a及任意不相等的实数x1、x2,都有n>0;
③对于任意的a,存在不相等的实数x1、x2,使得m=n;
④对于任意的a,存在不相等的实数x1、x2,使得m=﹣n.
其中的真命题有 ①④ (写出所有真命题的序号).
【考点】2K:命题的真假判断与应用.菁优网版权所有
【专题】2:创新题型;26:开放型;51:函数的性质及应用.
【分析】运用指数函数的单调性,即可判断①;由二次函数的单调性,即可判断②;
通过函数h(x)=x2+ax﹣2x,求出导数判断单调性,即可判断③;
通过函数h(x)=x2+ax+2x,求出导数判断单调性,即可判断④.
【解答】解:对于①,由于2>1,由指数函数的单调性可得f(x)在R上递增,即有m>0,则①正确;
对于②,由二次函数的单调性可得g(x)在(﹣∞,﹣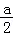 )递减,在(﹣
)递减,在(﹣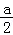 ,+∞)递增,则n>0不恒成立,
,+∞)递增,则n>0不恒成立,
则②错误;
对于③,由m=n,可得f(x1)﹣f(x2)=g(x1)﹣g(x2),即为g(x1)﹣f(x1)=g(x2)﹣f(x2),
考查函数h(x)=x2+ax﹣2x,h′(x)=2x+a﹣2xln2,
当a→﹣∞,h′(x)小于0,h(x)单调递减,则③错误;
对于④,由m=﹣n,可得f(x1)﹣f(x2)=﹣[g(x1)﹣g(x2)],考查函数h(x)=x2+ax+2x,
h′(x)=2x+a+2xln2,对于任意的a,h′(x)不恒大于0或小于0,则④正确.
故答案为:①④.
【点评】本题考查函数的单调性及运用,注意运用指数函数和二次函数的单调性,以及导数判断单调性是解题的关键.
三、解答题:本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤。
16.(12分)设数列{an}(n=1,2,3,…)的前n项和Sn满足Sn=2an﹣a1,且a1,a2+1,a3成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)记数列{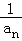 }的前n项和为Tn,求使得|Tn﹣1|
}的前n项和为Tn,求使得|Tn﹣1|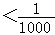 成立的n的最小值.
成立的n的最小值.
【考点】8E:数列的求和.菁优网版权所有
【专题】54:等差数列与等比数列.
【分析】(Ⅰ)由已知数列递推式得到an=2an﹣1(n≥2),再由已知a1,a2+1,a3成等差数列求出数列首项,可得数列{an}是首项为2,公比为2的等比数列,则其通项公式可求;
(Ⅱ)由(Ⅰ)求出数列{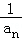 }的通项公式,再由等比数列的前n项和求得Tn,结合
}的通项公式,再由等比数列的前n项和求得Tn,结合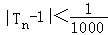 求解指数不等式得n的最小值.
求解指数不等式得n的最小值.
【解答】解:(Ⅰ)由已知Sn=2an﹣a1,有
an=Sn﹣Sn﹣1=2an﹣2an﹣1 (n≥2),
即an=2an﹣1(n≥2),
从而a2=2a1,a3=2a2=4a1,
又∵a1,a2+1,a3成等差数列,
∴a1+4a1=2(2a1+1),解得:a1=2.
∴数列{an}是首项为2,公比为2的等比数列.故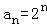 ;
;
(Ⅱ)由(Ⅰ)得: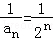 ,
,
∴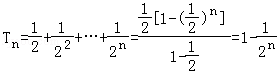 .
.
由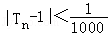 ,得
,得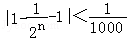 ,即2n>1000.
,即2n>1000.
∵29=512<1000<1024=210,
∴n≥10.
于是,使|Tn﹣1|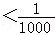 成立的n的最小值为10.
成立的n的最小值为10.
【点评】本题考查等差数列与等比数列的概念、等比数列的通项公式与前n项和公式等基础知识,考查运算求解能力,是中档题.
17.(12分)某市A、B两所中学的学生组队参加辩论赛,A中学推荐了3名男生、2名女生,B中学推荐了3名男生、4名女生,两校所推荐的学生一起参加集训.由于集训后队员水平相当,从参加集训的男生中随机抽取3人,女生中随机抽取3人组成代表队.
(Ⅰ)求A中学至少有1名学生入选代表队的概率;
(Ⅱ)某场比赛前,从代表队的6名队员中随机抽取4人参赛,设X表示参赛的男生人数,求X的分布列和数学期望.
【考点】CG:离散型随机变量及其分布列;CH:离散型随机变量的期望与方差.菁优网版权所有
【专题】5I:概率与统计.
【分析】(Ⅰ)求出A中学至少有1名学生入选代表队的对立事件的概率,然后求解概率即可;
(Ⅱ)求出X表示参赛的男生人数的可能值,求出概率,得到X的分布列,然后求解数学期望.
【解答】解:(Ⅰ)由题意,参加集训的男、女学生共有6人,参赛学生全从B中抽出(等价于A中没有学生入选代表队)的概率为: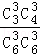 =
=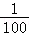 ,因此A中学至少有1名学生入选代表队的概率为:1﹣
,因此A中学至少有1名学生入选代表队的概率为:1﹣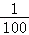 =
=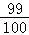 ;
;
(Ⅱ)某场比赛前,从代表队的6名队员中随机抽取4人参赛,X表示参赛的男生人数,
则X的可能取值为:1,2,3,
P(X=1)=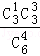 =
=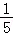 ,
,
P(X=2)=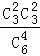 =
=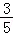 ,
,
P(X=3)=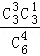 =
=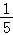 .
.
X的分布列:
X | 1 | 2 | 3 |
P | | | |
和数学期望EX=1×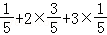 =2.
=2.
【点评】本题考查离散型随机变量的分布列,期望的求法,考查古典概型概率的求法,考查分析问题解决问题的能力.
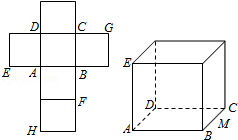
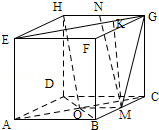
18.(12分)一个正方体的平面展开图及该正方体的直观图的示意图如图所示.在正方体中,设BC的中点为M、GH的中点为N.
(Ⅰ)请将字母F、G、H标记在正方体相应的顶点处(不需说明理由);
(Ⅱ)证明:直线MN∥平面BDH;
(Ⅲ)求二面角A﹣EG﹣M的余弦值.
【考点】LS:直线与平面平行;MJ:二面角的平面角及求法.菁优网版权所有
【专题】5F:空间位置关系与距离;5G:空间角.
【分析】(Ⅰ)根据展开图和直观图之间的关系进行判断即可;
(Ⅱ)利用线面平行的判定定理即可证明直线MN∥平面BDH;
(Ⅲ)法一:利用定义法求出二面角的平面角进行求解.
法二:建立坐标系,利用向量法进行求解即可.
【解答】解:(Ⅰ)F、G、H的位置如图;
证明:(Ⅱ)连接BD,设O是BD的中点,
∵BC的中点为M、GH的中点为N,
∴OM∥CD,OM=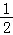 CD,
CD,
HN∥CD,HN=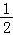 CD,
CD,
∴OM∥HN,OM=HN,
即四边形MNHO是平行四边形,
∴MN∥OH,
∵MN⊄平面BDH;OH⊂面BDH,
∴直线MN∥平面BDH;
(Ⅲ)方法一:
连接AC,过M作MH⊥AC于P,
则正方体ABCD﹣EFGH中,AC∥EG,
∴MP⊥EG,
过P作PK⊥EG于K,连接KM,
∴EG⊥平面PKM
则KM⊥EG,
则∠PKM是二面角A﹣EG﹣M的平面角,
设AD=2,则CM=1,PK=2,
在Rt△CMP中,PM=CMsin45°=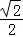 ,
,
在Rt△PKM中,KM=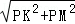 =
=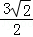 ,
,
∴cos∠PKM=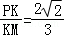 ,
,
即二面角A﹣EG﹣M的余弦值为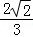 .
.
方法二:以D为坐标原点,
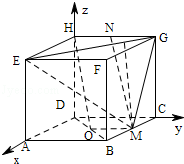
分别为DA,DC,DH方向为x,y,z轴建立空间坐标系如图:
设AD=2,则M(1,2,0),G(0,2,2),E(2,0,2),O(1,1,0),
则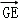 =(2,﹣2,0),
=(2,﹣2,0),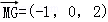 ,
,
设平面EGM的法向量为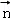 =(x,y,z),
=(x,y,z),
则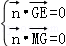 ,即
,即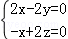 ,令x=2,得
,令x=2,得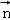 =(2,2,1),
=(2,2,1),
在正方体中,DO⊥平面AEGC,
则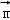 =
=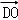 =(1,1,0)是平面AEG的一个法向量,
=(1,1,0)是平面AEG的一个法向量,
则cos<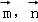 >=
>=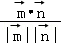 =
=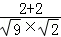 =
=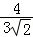 =
=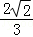 .
.
二面角A﹣EG﹣M的余弦值为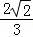 .
.
【点评】本题主要考查简单空间图形的直观图,空间线面平行的判定和性质,空间面面夹角的计算,考查空间想象能力,推理能力,运算求解能力.
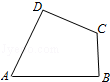
19.(12分)如图,A、B、C、D为平面四边形ABCD的四个内角.
(Ⅰ)证明:tan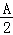 =
=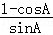 ;
;
(Ⅱ)若A+C=180°,AB=6,BC=3,CD=4,AD=5,求tan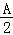 +tan
+tan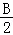 +tan
+tan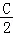 +tan
+tan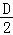 的值.
的值.
【考点】GJ:三角函数恒等式的证明.菁优网版权所有
【专题】57:三角函数的图像与性质;58:解三角形.
【分析】(Ⅰ)直接利用切化弦以及二倍角公式化简证明即可.
(Ⅱ)通过A+C=180°,得C=180°﹣A,D=180°﹣B,利用(Ⅰ)化简tan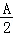 +tan
+tan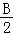 +tan
+tan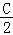 +tan
+tan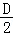 =
=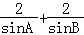 ,连结BD,在△ABD中,利用余弦定理求出sinA,连结AC,求出sinB,然后求解即可.
,连结BD,在△ABD中,利用余弦定理求出sinA,连结AC,求出sinB,然后求解即可.
【解答】证明:(Ⅰ)tan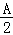 =
=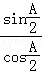 =
=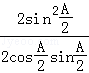 =
=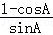 .等式成立.
.等式成立.
(Ⅱ)由A+C=180°,得C=180°﹣A,D=180°﹣B,由(Ⅰ)可知:tan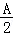 +tan
+tan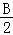 +tan
+tan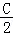 +tan
+tan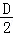 =
=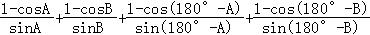 =
=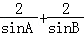 ,连结BD,在△ABD中,有BD2=AB2+AD2﹣2AB•ADcosA,AB=6,BC=3,CD=4,AD=5,
,连结BD,在△ABD中,有BD2=AB2+AD2﹣2AB•ADcosA,AB=6,BC=3,CD=4,AD=5,
在△BCD中,有BD2=BC2+CD2﹣2BC•CDcosC,
所以AB2+AD2﹣2AB•ADcosA=BC2+CD2﹣2BC•CDcosC,
则:cosA=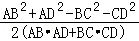 =
=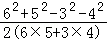 =
=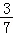 .
.
于是sinA=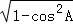 =
=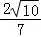 ,
,
连结AC,同理可得:cosB=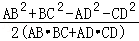 =
=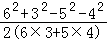 =
=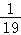 ,
,
于是sinB=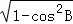 =
=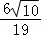 .
.
所以tan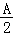 +tan
+tan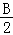 +tan
+tan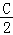 +tan
+tan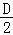 =
=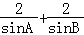 =
=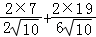 =
=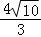 .
.
【点评】本题考查二倍角公式、诱导公式、余弦定理.简单的三角恒等变换,考查函数与方程的思想,转化与化归思想的应用.
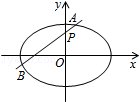
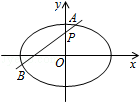
20.(13分)如图,椭圆E: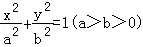 的离心率是
的离心率是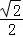 ,过点P(0,1)的动直线l与椭圆相交于A、B两点,当直线l平行于x轴时,直线l被椭圆E截得的线段长为2
,过点P(0,1)的动直线l与椭圆相交于A、B两点,当直线l平行于x轴时,直线l被椭圆E截得的线段长为2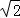 .
.
(Ⅰ)求椭圆E的方程;
(Ⅱ)在平面直角坐标系xOy中,是否存在与点P不同的定点Q,使得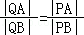 恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
【考点】K3:椭圆的标准方程;KH:直线与圆锥曲线的综合.菁优网版权所有
【专题】2:创新题型;5D:圆锥曲线的定义、性质与方程.
【分析】(Ⅰ)通过直线l平行于x轴时被椭圆E截得的线段长为2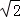 及离心率是
及离心率是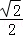 ,计算即得结论;
,计算即得结论;
(Ⅱ)通过直线l与x轴平行、垂直时,可得若存在不同于点P的定点Q满足条件,则Q点坐标只能是(0,2).然后分直线l的斜率不存在、存在两种情况,利用韦达定理及直线斜率计算方法,证明对任意直线l,均有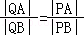 即可.
即可.
【解答】解:(Ⅰ)∵直线l平行于x轴时,直线l被椭圆E截得的线段长为2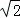 ,
,
∴点(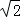 ,1)在椭圆E上,
,1)在椭圆E上,
又∵离心率是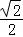 ,
,
∴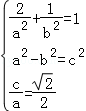 ,解得a=2,b=
,解得a=2,b=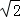 ,
,
∴椭圆E的方程为: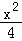 +
+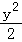 =1;
=1;
(Ⅱ)结论:存在与点P不同的定点Q(0,2),使得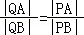 恒成立.
恒成立.
理由如下:
当直线l与x轴平行时,设直线l与椭圆相交于C、D两点,
如果存在定点Q满足条件,则有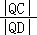 =
= =1,即|QC|=|QD|.
=1,即|QC|=|QD|.
∴Q点在直线y轴上,可设Q(0,y0).
当直线l与x轴垂直时,设直线l与椭圆相交于M、N两点,
则M、N的坐标分别为(0,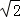 )、(0,﹣
)、(0,﹣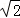 ),
),
又∵ =
= ,∴
,∴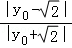 =
=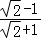 ,解得y0=1或y0=2.
,解得y0=1或y0=2.
∴若存在不同于点P的定点Q满足条件,则Q点坐标只能是(0,2).
下面证明:对任意直线l,均有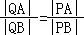 .
.
当直线l的斜率不存在时,由上可知,结论成立.
当直线l的斜率存在时,可设直线l的方程为y=kx+1,
A、B的坐标分别为A(x1,y1)、B(x2,y2),
联立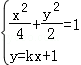 ,消去y并整理得:(1+2k2)x2+4kx﹣2=0,
,消去y并整理得:(1+2k2)x2+4kx﹣2=0,
∵△=(4k)2+8(1+2k2)>0,
∴x1+x2=﹣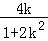 ,x1x2=﹣
,x1x2=﹣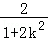 ,
,
∴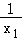 +
+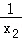 =
=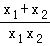 =2k,
=2k,
已知点B关于y轴对称的点B′的坐标为(﹣x2,y2),
又kAQ=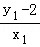 =
=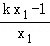 =k﹣
=k﹣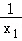 ,kQB′=
,kQB′=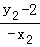 =
=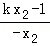 =﹣k+
=﹣k+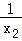 =k﹣
=k﹣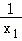 ,
,
∴kAQ=kQB′,即Q、A、B′三点共线,
∴ =
=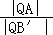 =
=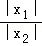 =
= .
.
故存在与点P不同的定点Q(0,2),使得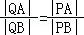 恒成立.
恒成立.

【点评】本题考查椭圆的标准方程与几何性质、直线方程、直线与椭圆的位置关系等基础知识,考查推理论证能力、运算求解能力,考查数形结合、化归与转化、特殊与一般、分类与整合等数学思想,注意解题方法的积累,属于难题.
21.(14分)已知函数f(x)=﹣2(x+a)lnx+x2﹣2ax﹣2a2+a,其中a>0.
(Ⅰ)设g(x)是f(x)的导函数,讨论g(x)的单调性;
(Ⅱ)证明:存在a∈(0,1),使得f(x)≥0在区间(1,+∞)内恒成立,且f(x)=0在区间(1,+∞)内有唯一解.
【考点】6B:利用导数研究函数的单调性;6E:利用导数研究函数的最值.菁优网版权所有
【专题】2:创新题型;53:导数的综合应用.
【分析】(Ⅰ)求出函数f(x)的定义域,把函数f(x)求导得到g(x)再对g(x)求导,得到其导函数的零点,然后根据导函数在各区间段内的符号得到函数g(x)的单调期间;
(Ⅱ)由f(x)的导函数等于0把a用含有x的代数式表示,然后构造函数φ(x)=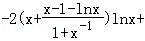 x2
x2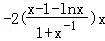
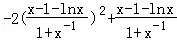 ,由函数零点存在定理得到x0∈(1,e),使得φ(x0)=0.令
,由函数零点存在定理得到x0∈(1,e),使得φ(x0)=0.令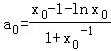 ,u(x)=x﹣1﹣lnx(x≥1),利用导数求得a0∈(0,1),然后进一步利用导数说明当a=a0时,若x∈(1,+∞),有f(x)≥0,即可得到存在a∈(0,1),使得f(x)≥0在区间(1,+∞)内恒成立,且f(x)=0在区间(1,+∞)内有唯一解.
,u(x)=x﹣1﹣lnx(x≥1),利用导数求得a0∈(0,1),然后进一步利用导数说明当a=a0时,若x∈(1,+∞),有f(x)≥0,即可得到存在a∈(0,1),使得f(x)≥0在区间(1,+∞)内恒成立,且f(x)=0在区间(1,+∞)内有唯一解.
【解答】解:(Ⅰ)由已知,函数f(x)的定义域为(0,+∞),
g(x)=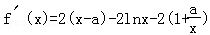 ,
,
∴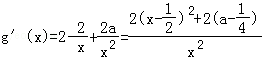 .
.
当0<a<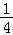 时,g(x)在
时,g(x)在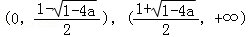 上单调递增,
上单调递增,
在区间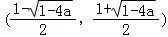 上单调递减;
上单调递减;
当a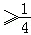 时,g(x)在(0,+∞)上单调递增.
时,g(x)在(0,+∞)上单调递增.
(Ⅱ)由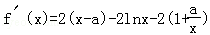 =0,解得
=0,解得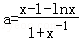 ,
,
令φ(x)=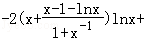 x2
x2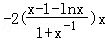
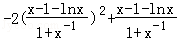 ,
,
则φ(1)=1>0,φ(e)=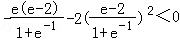 .
.
故存在x0∈(1,e),使得φ(x0)=0.
令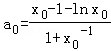 ,u(x)=x﹣1﹣lnx(x≥1),
,u(x)=x﹣1﹣lnx(x≥1),
由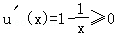 知,函数u(x)在(1,+∞)上单调递增.
知,函数u(x)在(1,+∞)上单调递增.
∴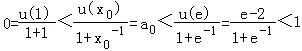 .
.
即a0∈(0,1),
当a=a0时,有f′(x0)=0,f(x0)=φ(x0)=0.
由(Ⅰ)知,f′(x)在(1,+∞)上单调递增,
故当x∈(1,x0)时,f′(x)<0,从而f(x)>f(x0)=0;
当x∈(x0,+∞)时,f′(x)>0,从而f(x)>f(x0)=0.
∴当x∈(1,+∞)时,f(x)≥0.
综上所述,存在a∈(0,1),使得f(x)≥0在区间(1,+∞)内恒成立,且f(x)=0在区间(1,+∞)内有唯一解.
【点评】本题主要考查导数的运算、导数在研究函数中的应用、函数零点等基础知识,考查推理论证能力、运算求解能力、创新知识,考查了函数与方程、数形结合、分类与整合、化归与转化等数学思想方法,是压轴题.