2017年全国普通高考 文科数学试题及参考答案
点击“下载文件”,可以下载PDF
2017年四川省高考数学试卷
(文科)(新课标Ⅲ)
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5分)已知集合A={1,2,3,4},B={2,4,6,8},则A∩B中元素的个数为( )
A.1B.2 C.3 D.4
2.(5分)复平面内表示复数z=i(﹣2+i)的点位于( )
A.第一象限B.第二象限 C.第三象限 D.第四象限
3.(5分)某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.
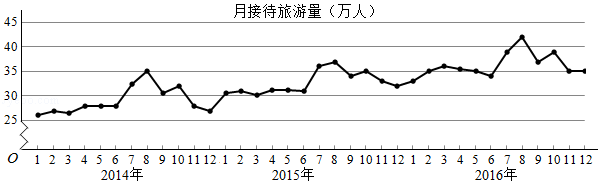
根据该折线图,下列结论错误的是( )
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
4.(5分)已知sinα﹣cosα=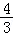 ,则sin2α=( )
,则sin2α=( )
A.﹣B.﹣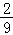 C.
C.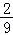 D.
D.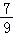
5.(5分)设x,y满足约束条件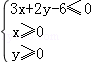 则z=x﹣y的取值范围是( )
则z=x﹣y的取值范围是( )
A.[﹣3,0]B.[﹣3,2] C.[0,2] D.[0,3]
6.(5分)函数f(x)=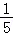 sin(x+
sin(x+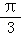 )+cos(x﹣
)+cos(x﹣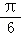 )的最大值为( )
)的最大值为( )
A.B.1 C. D.
D.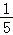
7.(5分)函数y=1+x+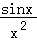 的部分图象大致为( )
的部分图象大致为( )
A.

B.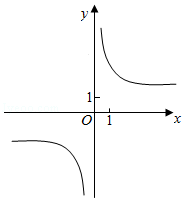
C.
D.
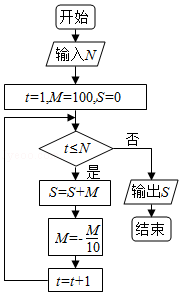
8.(5分)执行如图的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为( )
A.5B.4 C.3 D.2
9.(5分)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )
A.πB. C.
C. D.
D.
10.(5分)在正方体ABCD﹣A1B1C1D1中,E为棱CD的中点,则( )
A.A1E⊥DC1B.A1E⊥BD C.A1E⊥BC1 D.A1E⊥AC
11.(5分)已知椭圆C: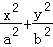 =1(a>b>0)的左、右顶点分别为A1,A2,且以线段A1A2为直径的圆与直线bx﹣ay+2ab=0相切,则C的离心率为( )
=1(a>b>0)的左、右顶点分别为A1,A2,且以线段A1A2为直径的圆与直线bx﹣ay+2ab=0相切,则C的离心率为( )
A.B.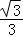 C.
C.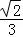 D.
D.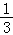
12.(5分)已知函数f(x)=x2﹣2x+a(ex﹣1+e﹣x+1)有唯一零点,则a=( )
A.﹣B.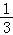 C.
C. D.1
D.1
二、填空题
13.(5分)已知向量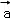 =(﹣2,3),
=(﹣2,3),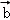 =(3,m),且
=(3,m),且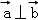 ,则m= .
,则m= .
14.(5分)双曲线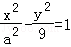 (a>0)的一条渐近线方程为y=
(a>0)的一条渐近线方程为y=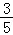 x,则a= .
x,则a= .
15.(5分)△ABC的内角A,B,C的对边分别为a,b,c,已知C=60°,b=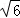 ,c=3,则A= .
,c=3,则A= .
16.(5分)设函数f(x)=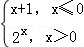 ,则满足f(x)+f(x﹣
,则满足f(x)+f(x﹣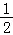 )>1的x的取值范围是 .
)>1的x的取值范围是 .
三、解答题
17.(12分)设数列{an}满足a1+3a2+…+(2n﹣1)an=2n.
(1)求{an}的通项公式;
(2)求数列{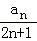 }的前n项和.
}的前n项和.
18.(12分)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)求六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.
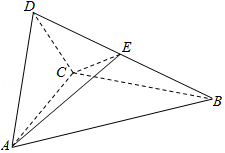
19.(12分)如图四面体ABCD中,△ABC是正三角形,AD=CD.
(1)证明:AC⊥BD;
(2)已知△ACD是直角三角形,AB=BD,若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.
20.(12分)在直角坐标系xOy中,曲线y=x2+mx﹣2与x轴交于A、B两点,点C的坐标为(0,1),当m变化时,解答下列问题:
(1)能否出现AC⊥BC的情况?说明理由;
(2)证明过A、B、C三点的圆在y轴上截得的弦长为定值.
21.(12分)已知函数f(x)=lnx+ax2+(2a+1)x.
(1)讨论f(x)的单调性;
(2)当a<0时,证明f(x)≤﹣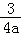 ﹣2.
﹣2.
[选修4-4:坐标系与参数方程]
22.(10分)在直角坐标系xOy中,直线l1的参数方程为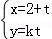 ,(t为参数),直线l2的参数方程为
,(t为参数),直线l2的参数方程为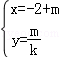 ,(m为参数).设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
,(m为参数).设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
(1)写出C的普通方程;
(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ)﹣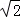 =0,M为l3与C的交点,求M的极径.
=0,M为l3与C的交点,求M的极径.
[选修4-5:不等式选讲]
23.已知函数f(x)=|x+1|﹣|x﹣2|.
(1)求不等式f(x)≥1的解集;
(2)若不等式f(x)≥x2﹣x+m的解集非空,求m的取值范围.
2017年四川省高考数学试卷(文科)(新课标Ⅲ)
参考答案与试题解析
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5分)已知集合A={1,2,3,4},B={2,4,6,8},则A∩B中元素的个数为( )
A.1B.2 C.3 D.4
【考点】1E:交集及其运算.菁优网版权所有
【专题】11:计算题;37:集合思想;4O:定义法;5J:集合.
【分析】利用交集定义先求出A∩B,由此能求出A∩B中元素的个数.
【解答】解:∵集合A={1,2,3,4},B={2,4,6,8},
∴A∩B={2,4},
∴A∩B中元素的个数为2.
故选:B.
【点评】本题考查交集中元素个数的求法,是基础题,解题时要认真审题,注意交集定义的合理运用.
2.(5分)复平面内表示复数z=i(﹣2+i)的点位于( )
A.第一象限B.第二象限 C.第三象限 D.第四象限
【考点】A4:复数的代数表示法及其几何意义.菁优网版权所有
【专题】35:转化思想;5N:数系的扩充和复数.
【分析】利用复数的运算法则、几何意义即可得出.
【解答】解:z=i(﹣2+i)=﹣2i﹣1对应的点(﹣1,﹣2)位于第三象限.
故选:C.
【点评】本题考查了复数的运算法则、几何意义,考查了推理能力与计算能力,属于基础题.
3.(5分)某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.
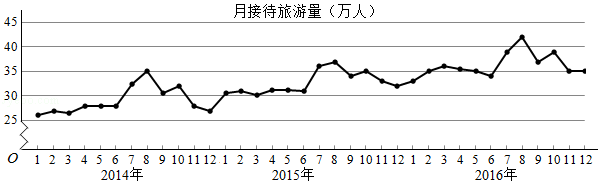
根据该折线图,下列结论错误的是( )
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
【考点】2K:命题的真假判断与应用;B9:频率分布折线图、密度曲线.菁优网版权所有
【专题】27:图表型;2A:探究型;5I:概率与统计.
【分析】根据已知中2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,逐一分析给定四个结论的正误,可得答案.
【解答】解:由已有中2014年1月至2016年12月期间月接待游客量(单位:万人)的数据可得:
月接待游客量逐月有增有减,故A错误;
年接待游客量逐年增加,故B正确;
各年的月接待游客量高峰期大致在7,8月,故C正确;
各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳,故D正确;
故选:A.
【点评】本题考查的知识点是数据的分析,命题的真假判断与应用,难度不大,属于基础题.
4.(5分)已知sinα﹣cosα=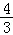 ,则sin2α=( )
,则sin2α=( )
A.﹣B.﹣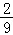 C.
C.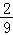 D.
D.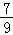
【考点】GS:二倍角的三角函数.菁优网版权所有
【专题】11:计算题;35:转化思想;4O:定义法;56:三角函数的求值.
【分析】由条件,两边平方,根据二倍角公式和平方关系即可求出.
【解答】解:∵sinα﹣cosα=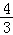 ,
,
∴(sinα﹣cosα)2=1﹣2sinαcosα=1﹣sin2α=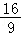 ,
,
∴sin2α=﹣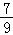 ,
,
故选:A.
【点评】本题考查了二倍角公式,属于基础题.
5.(5分)设x,y满足约束条件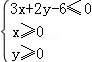 则z=x﹣y的取值范围是( )
则z=x﹣y的取值范围是( )
A.[﹣3,0]B.[﹣3,2] C.[0,2] D.[0,3]
【考点】7C:简单线性规划.菁优网版权所有
【专题】11:计算题;31:数形结合;35:转化思想;5T:不等式.
【分析】画出约束条件的可行域,利用目标函数的最优解求解目标函数的范围即可.
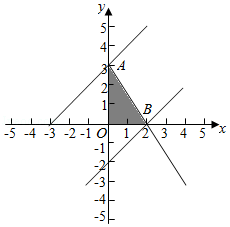
【解答】解:x,y满足约束条件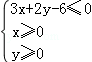 的可行域如图:
的可行域如图:
目标函数z=x﹣y,经过可行域的A,B时,目标函数取得最值,
由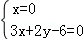 解得A(0,3),
解得A(0,3),
由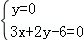 解得B(2,0),
解得B(2,0),
目标函数的最大值为:2,最小值为:﹣3,
目标函数的取值范围:[﹣3,2].
故选:B.
【点评】本题考查线性规划的简单应用,目标函数的最优解以及可行域的作法是解题的关键.
6.(5分)函数f(x)=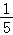 sin(x+
sin(x+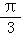 )+cos(x﹣
)+cos(x﹣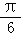 )的最大值为( )
)的最大值为( )
A.B.1 C.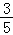 D.
D.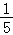
【考点】HW:三角函数的最值.菁优网版权所有
【专题】11:计算题;35:转化思想;49:综合法;57:三角函数的图像与性质.
【分析】利用诱导公式化简函数的解析式,通过正弦函数的最值求解即可.
【解答】解:函数f(x)=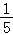 sin(x+
sin(x+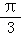 )+cos(x﹣
)+cos(x﹣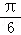 )=
)=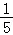 sin(x+
sin(x+ )+cos(﹣x+
)+cos(﹣x+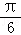 )=
)=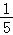 sin(x+
sin(x+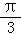 )+sin(x+
)+sin(x+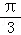 )
)
=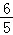 sin(x+
sin(x+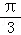 )
)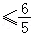 .
.
故选:A.
【点评】本题考查诱导公式的应用,三角函数的最值,正弦函数的有界性,考查计算能力.
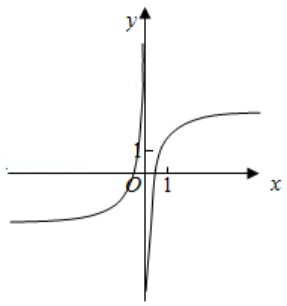
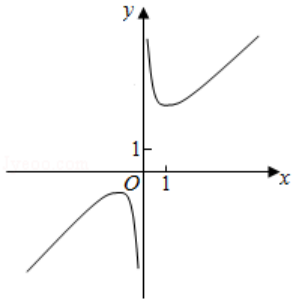
7.(5分)函数y=1+x+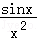 的部分图象大致为( )
的部分图象大致为( )
A.

B.
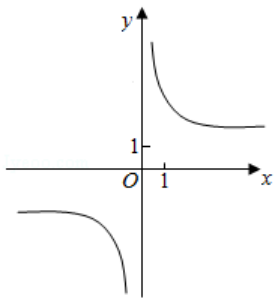
C.
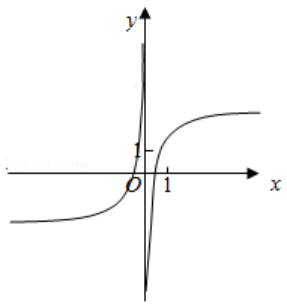
D.
【考点】3A:函数的图象与图象的变换.菁优网版权所有
【专题】11:计算题;31:数形结合;35:转化思想;51:函数的性质及应用.
【分析】通过函数的解析式,利用函数的奇偶性的性质,函数的图象经过的特殊点判断函数的图象即可.
【解答】解:函数y=1+x+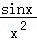 ,可知:f(x)=x+
,可知:f(x)=x+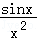 是奇函数,所以函数的图象关于原点对称,
是奇函数,所以函数的图象关于原点对称,
则函数y=1+x+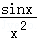 的图象关于(0,1)对称,
的图象关于(0,1)对称,
当x→0+,f(x)>0,排除A、C,当x=π时,y=1+π,排除B.
故选:D.
【点评】本题考查函数的图象的判断,函数的奇偶性以及特殊点是常用方法.
8.(5分)执行如图的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为( )
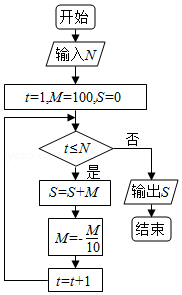
A.5B.4 C.3 D.2
【考点】EF:程序框图.菁优网版权所有
【专题】11:计算题;39:运动思想;49:综合法;5K:算法和程序框图.
【分析】通过模拟程序,可得到S的取值情况,进而可得结论.
【解答】解:由题可知初始值t=1,M=100,S=0,
要使输出S的值小于91,应满足“t≤N”,
则进入循环体,从而S=100,M=﹣10,t=2,
要使输出S的值小于91,应接着满足“t≤N”,
则进入循环体,从而S=90,M=1,t=3,
要使输出S的值小于91,应不满足“t≤N”,跳出循环体,
此时N的最小值为2,
故选:D.
【点评】本题考查程序框图,判断出什么时候跳出循环体是解决本题的关键,注意解题方法的积累,属于中档题.
9.(5分)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )
A.πB.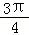 C.
C.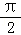 D.
D.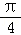
【考点】LF:棱柱、棱锥、棱台的体积;LR:球内接多面体.菁优网版权所有
【专题】11:计算题;34:方程思想;4O:定义法;5Q:立体几何.
【分析】推导出该圆柱底面圆周半径r=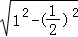 =
=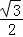 ,由此能求出该圆柱的体积.
,由此能求出该圆柱的体积.
【解答】解:∵圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,
∴该圆柱底面圆周半径r=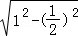 =
=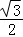 ,
,
∴该圆柱的体积:V=Sh=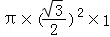 =
= .
.
故选:B.
【点评】本题考查面圆柱的体积的求法,考查圆柱、球等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想,是中档题.
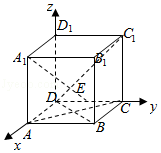
10.(5分)在正方体ABCD﹣A1B1C1D1中,E为棱CD的中点,则( )
A.A1E⊥DC1B.A1E⊥BD C.A1E⊥BC1 D.A1E⊥AC
【考点】LO:空间中直线与直线之间的位置关系.菁优网版权所有
【专题】11:计算题;31:数形结合;41:向量法;5G:空间角.
【分析】法一:连B1C,推导出BC1⊥B1C,A1B1⊥BC1,从而BC1⊥平面A1ECB1,由此得到A1E⊥BC1.
法二:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出结果.
【解答】解:法一:连B1C,由题意得BC1⊥B1C,
∵A1B1⊥平面B1BCC1,且BC1⊂平面B1BCC1,
∴A1B1⊥BC1,
∵A1B1∩B1C=B1,
∴BC1⊥平面A1ECB1,
∵A1E⊂平面A1ECB1,
∴A1E⊥BC1.
故选:C.
法二:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设正方体ABCD﹣A1B1C1D1中棱长为2,
则A1(2,0,2),E(0,1,0),B(2,2,0),D(0,0,0),C1(0,2,2),A(2,0,0),C(0,2,0),
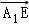 =(﹣2,1,﹣2),
=(﹣2,1,﹣2),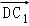 =(0,2,2),
=(0,2,2),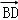 =(﹣2,﹣2,0),
=(﹣2,﹣2,0),
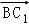 =(﹣2,0,2),
=(﹣2,0,2),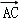 =(﹣2,2,0),
=(﹣2,2,0),
∵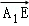 •
•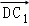 =﹣2,
=﹣2,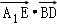 =2,
=2,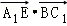 =0,
=0,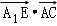 =6,
=6,
∴A1E⊥BC1.
故选:C.
【点评】本题考查线线垂直的判断,是中档题,解题时要认真审题,注意向量法的合理运用.
11.(5分)已知椭圆C: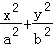 =1(a>b>0)的左、右顶点分别为A1,A2,且以线段A1A2为直径的圆与直线bx﹣ay+2ab=0相切,则C的离心率为( )
=1(a>b>0)的左、右顶点分别为A1,A2,且以线段A1A2为直径的圆与直线bx﹣ay+2ab=0相切,则C的离心率为( )
A.B.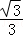 C.
C.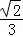 D.
D.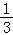
【考点】K4:椭圆的性质.菁优网版权所有
【专题】34:方程思想;5B:直线与圆;5D:圆锥曲线的定义、性质与方程.
【分析】以线段A1A2为直径的圆与直线bx﹣ay+2ab=0相切,可得原点到直线的距离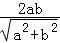 =a,化简即可得出.
=a,化简即可得出.
【解答】解:以线段A1A2为直径的圆与直线bx﹣ay+2ab=0相切,
∴原点到直线的距离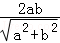 =a,化为:a2=3b2.
=a,化为:a2=3b2.
∴椭圆C的离心率e=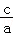 =
=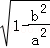 =
=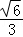 .
.
故选:A.
【点评】本题考查了椭圆的标准方程及其性质、直线与圆相切的性质、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.
12.(5分)已知函数f(x)=x2﹣2x+a(ex﹣1+e﹣x+1)有唯一零点,则a=( )
A.﹣B.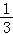 C.
C.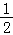 D.1
D.1
【考点】52:函数零点的判定定理.菁优网版权所有
【专题】11:计算题;33:函数思想;49:综合法;51:函数的性质及应用.
【分析】通过转化可知问题等价于函数y=1﹣(x﹣1)2的图象与y=a(ex﹣1+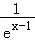 )的图象只有一个交点求a的值.分a=0、a<0、a>0三种情况,结合函数的单调性分析可得结论.
)的图象只有一个交点求a的值.分a=0、a<0、a>0三种情况,结合函数的单调性分析可得结论.
【解答】解:因为f(x)=x2﹣2x+a(ex﹣1+e﹣x+1)=﹣1+(x﹣1)2+a(ex﹣1+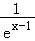 )=0,
)=0,
所以函数f(x)有唯一零点等价于方程1﹣(x﹣1)2=a(ex﹣1+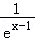 )有唯一解,
)有唯一解,
等价于函数y=1﹣(x﹣1)2的图象与y=a(ex﹣1+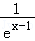 )的图象只有一个交点.
)的图象只有一个交点.
①当a=0时,f(x)=x2﹣2x≥﹣1,此时有两个零点,矛盾;
②当a<0时,由于y=1﹣(x﹣1)2在(﹣∞,1)上递增、在(1,+∞)上递减,
且y=a(ex﹣1+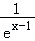 )在(﹣∞,1)上递增、在(1,+∞)上递减,
)在(﹣∞,1)上递增、在(1,+∞)上递减,
所以函数y=1﹣(x﹣1)2的图象的最高点为A(1,1),y=a(ex﹣1+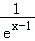 )的图象的最高点为B(1,2a),
)的图象的最高点为B(1,2a),
由于2a<0<1,此时函数y=1﹣(x﹣1)2的图象与y=a(ex﹣1+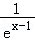 )的图象有两个交点,矛盾;
)的图象有两个交点,矛盾;
③当a>0时,由于y=1﹣(x﹣1)2在(﹣∞,1)上递增、在(1,+∞)上递减,
且y=a(ex﹣1+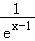 )在(﹣∞,1)上递减、在(1,+∞)上递增,
)在(﹣∞,1)上递减、在(1,+∞)上递增,
所以函数y=1﹣(x﹣1)2的图象的最高点为A(1,1),y=a(ex﹣1+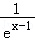 )的图象的最低点为B(1,2a),
)的图象的最低点为B(1,2a),
由题可知点A与点B重合时满足条件,即2a=1,即a=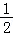 ,符合条件;
,符合条件;
综上所述,a=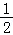 ,
,
故选:C.
【点评】本题考查函数零点的判定定理,考查函数的单调性,考查运算求解能力,考查数形结合能力,考查转化与化归思想,考查分类讨论的思想,注意解题方法的积累,属于难题.
二、填空题
13.(5分)已知向量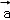 =(﹣2,3),
=(﹣2,3), =(3,m),且
=(3,m),且 ,则m= 2 .
,则m= 2 .
【考点】9T:数量积判断两个平面向量的垂直关系.菁优网版权所有
【专题】11:计算题;34:方程思想;4O:定义法;5A:平面向量及应用.
【分析】利用平面向量数量积坐标运算法则和向量垂直的性质求解.
【解答】解:∵向量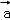 =(﹣2,3),
=(﹣2,3),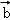 =(3,m),且
=(3,m),且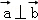 ,
,
∴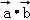 =﹣6+3m=0,
=﹣6+3m=0,
解得m=2.
故答案为:2.
【点评】本题考查实数值的求法,是基础题,解题时要认真审题,注意平面向量数量积坐标运算法则和向量垂直的性质的合理运用.
14.(5分)双曲线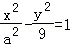 (a>0)的一条渐近线方程为y=
(a>0)的一条渐近线方程为y=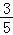 x,则a= 5 .
x,则a= 5 .
【考点】KC:双曲线的性质.菁优网版权所有
【专题】11:计算题;35:转化思想;5D:圆锥曲线的定义、性质与方程.
【分析】利用双曲线方程,求出渐近线方程,求解a即可.
【解答】解:双曲线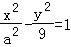 (a>0)的一条渐近线方程为y=
(a>0)的一条渐近线方程为y=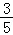 x,
x,
可得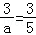 ,解得a=5.
,解得a=5.
故答案为:5.
【点评】本题考查双曲线的简单性质的应用,考查计算能力.
15.(5分)△ABC的内角A,B,C的对边分别为a,b,c,已知C=60°,b=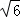 ,c=3,则A= 75° .
,c=3,则A= 75° .
【考点】HP:正弦定理;HR:余弦定理.菁优网版权所有
【专题】11:计算题;35:转化思想;4O:定义法;58:解三角形.
【分析】根据正弦定理和三角形的内角和计算即可
【解答】解:根据正弦定理可得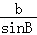 =
=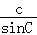 ,C=60°,b=
,C=60°,b=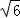 ,c=3,
,c=3,
∴sinB=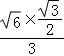 =
=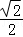 ,
,
∵b<c,
∴B=45°,
∴A=180°﹣B﹣C=180°﹣45°﹣60°=75°,
故答案为:75°.
【点评】本题考查了三角形的内角和以及正弦定理,属于基础题
16.(5分)设函数f(x)= ,则满足f(x)+f(x﹣
,则满足f(x)+f(x﹣ )>1的x的取值范围是 (
)>1的x的取值范围是 (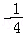 ,+∞) .
,+∞) .
【考点】3T:函数的值.菁优网版权所有
【专题】32:分类讨论;4R:转化法;51:函数的性质及应用.
【分析】根据分段函数的表达式,分别讨论x的取值范围,进行求解即可.
【解答】解:若x≤0,则x﹣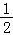 ≤﹣
≤﹣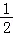 ,
,
则f(x)+f(x﹣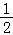 )>1等价为x+1+x﹣
)>1等价为x+1+x﹣ +1>1,即2x>﹣
+1>1,即2x>﹣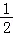 ,则x>
,则x> ,
,
此时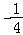 <x≤0,
<x≤0,
当x>0时,f(x)=2x>1,x﹣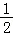 >﹣
>﹣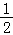 ,
,
当x﹣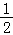 >0即x>
>0即x>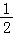 时,满足f(x)+f(x﹣
时,满足f(x)+f(x﹣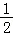 )>1恒成立,
)>1恒成立,
当0≥x﹣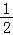 >﹣
>﹣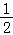 ,即
,即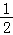 ≥x>0时,f(x﹣
≥x>0时,f(x﹣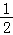 )=x﹣
)=x﹣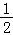 +1=x+
+1=x+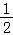
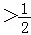 ,
,
此时f(x)+f(x﹣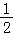 )>1恒成立,
)>1恒成立,
综上x>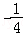 ,
,
故答案为:(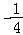 ,+∞).
,+∞).
【点评】本题主要考查不等式的求解,结合分段函数的不等式,利用分类讨论的数学思想进行求解是解决本题的关键.
三、解答题
17.(12分)设数列{an}满足a1+3a2+…+(2n﹣1)an=2n.
(1)求{an}的通项公式;
(2)求数列{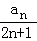 }的前n项和.
}的前n项和.
【考点】8E:数列的求和;8H:数列递推式.菁优网版权所有
【专题】34:方程思想;35:转化思想;54:等差数列与等比数列.
【分析】(1)利用数列递推关系即可得出.
(2)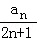 =
=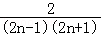 =
=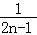 ﹣
﹣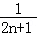 .利用裂项求和方法即可得出.
.利用裂项求和方法即可得出.
【解答】解:(1)数列{an}满足a1+3a2+…+(2n﹣1)an=2n.
n≥2时,a1+3a2+…+(2n﹣3)an﹣1=2(n﹣1).
∴(2n﹣1)an=2.∴an=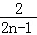 .
.
当n=1时,a1=2,上式也成立.
∴an=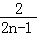 .
.
(2)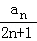 =
=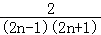 =
=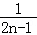 ﹣
﹣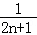 .
.
∴数列{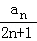 }的前n项和=
}的前n项和=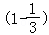 +
+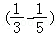 +…+
+…+ =1﹣
=1﹣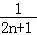 =
=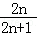 .
.
【点评】本题考查了数列递推关系、裂项求和方法,考查了推理能力与计算能力,属于中档题.
18.(12分)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)求六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.
【考点】CB:古典概型及其概率计算公式;CH:离散型随机变量的期望与方差.菁优网版权所有
【专题】11:计算题;35:转化思想;49:综合法;5I:概率与统计.
【分析】(1)由前三年六月份各天的最高气温数据,求出最高气温位于区间[20,25)和最高气温低于20的天数,由此能求出六月份这种酸奶一天的需求量不超过300瓶的概率.
(2)当温度大于等于25°C时,需求量为500,求出Y=900元;当温度在[20,25)°C时,需求量为300,求出Y=300元;当温度低于20°C时,需求量为200,求出Y=﹣100元,从而当温度大于等于20时,Y>0,由此能估计估计Y大于零的概率.
【解答】解:(1)由前三年六月份各天的最高气温数据,
得到最高气温位于区间[20,25)和最高气温低于20的天数为2+16+36=54,
根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.
如果最高气温不低于25,需求量为500瓶,
如果最高气温位于区间[20,25),需求量为300瓶,
如果最高气温低于20,需求量为200瓶,
∴六月份这种酸奶一天的需求量不超过300瓶的概率p=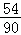 =
= .
.
(2)当温度大于等于25°C时,需求量为500,
Y=450×2=900元,
当温度在[20,25)°C时,需求量为300,
Y=300×2﹣(450﹣300)×2=300元,
当温度低于20°C时,需求量为200,
Y=400﹣(450﹣200)×2=﹣100元,
当温度大于等于20时,Y>0,
由前三年六月份各天的最高气温数据,得当温度大于等于20°C的天数有:
90﹣(2+16)=72,
∴估计Y大于零的概率P=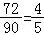 .
.
【点评】本题考查概率的求法,考查利润的所有可能取值的求法,考查函数、古典概型等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查数形结合思想、化归与转化思想,是中档题.
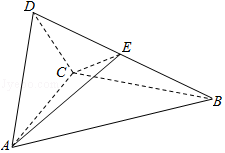
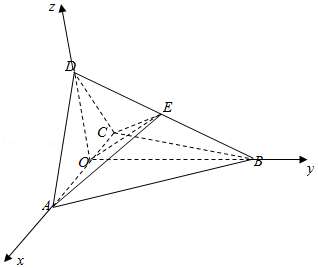
19.(12分)如图四面体ABCD中,△ABC是正三角形,AD=CD.
(1)证明:AC⊥BD;
(2)已知△ACD是直角三角形,AB=BD,若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.
【考点】LF:棱柱、棱锥、棱台的体积;LW:直线与平面垂直.菁优网版权所有
【专题】11:计算题;31:数形结合;41:向量法;5F:空间位置关系与距离.
【分析】(1)取AC中点O,连结DO、BO,推导出DO⊥AC,BO⊥AC,从而AC⊥平面BDO,由此能证明AC⊥BD.
(2)法一:连结OE,设AD=CD=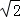 ,则OC=OA=1,由余弦定理求出BE=1,由BE=ED,四面体ABCE与四面体ACDE的高都是点A到平面BCD的高h,S△DCE=S△BCE,由此能求出四面体ABCE与四面体ACDE的体积比.法二:设AD=CD=
,则OC=OA=1,由余弦定理求出BE=1,由BE=ED,四面体ABCE与四面体ACDE的高都是点A到平面BCD的高h,S△DCE=S△BCE,由此能求出四面体ABCE与四面体ACDE的体积比.法二:设AD=CD=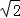 ,则AC=AB=BC=BD=2,AO=CO=DO=1,BO=
,则AC=AB=BC=BD=2,AO=CO=DO=1,BO=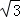 ,推导出BO⊥DO,以O为原点,OA为x轴,OB为y轴,OD为z轴,建立空间直角坐标系,由AE⊥EC,求出DE=BE,由此能求出四面体ABCE与四面体ACDE的体积比.
,推导出BO⊥DO,以O为原点,OA为x轴,OB为y轴,OD为z轴,建立空间直角坐标系,由AE⊥EC,求出DE=BE,由此能求出四面体ABCE与四面体ACDE的体积比.
【解答】证明:(1)取AC中点O,连结DO、BO,
∵△ABC是正三角形,AD=CD,
∴DO⊥AC,BO⊥AC,
∵DO∩BO=O,∴AC⊥平面BDO,
∵BD⊂平面BDO,∴AC⊥BD.
解:(2)法一:连结OE,由(1)知AC⊥平面OBD,
∵OE⊂平面OBD,∴OE⊥AC,
设AD=CD=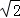 ,则OC=OA=1,EC=EA,
,则OC=OA=1,EC=EA,
∵AE⊥CE,AC=2,∴EC2+EA2=AC2,
∴EC=EA=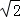 =CD,
=CD,
∴E是线段AC垂直平分线上的点,∴EC=EA=CD=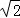 ,
,
由余弦定理得:
cos∠CBD=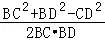 =
=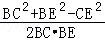 ,
,
即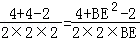 ,解得BE=1或BE=2,
,解得BE=1或BE=2,
∵BE<<BD=2,∴BE=1,∴BE=ED,
∵四面体ABCE与四面体ACDE的高都是点A到平面BCD的高h,
∵BE=ED,∴S△DCE=S△BCE,
∴四面体ABCE与四面体ACDE的体积比为1.
法二:设AD=CD=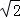 ,则AC=AB=BC=BD=2,AO=CO=DO=1,
,则AC=AB=BC=BD=2,AO=CO=DO=1,
∴BO=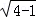 =
=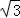 ,∴BO2+DO2=BD2,∴BO⊥DO,
,∴BO2+DO2=BD2,∴BO⊥DO,
以O为原点,OA为x轴,OB为y轴,OD为z轴,建立空间直角坐标系,
则C(﹣1,0,0),D(0,0,1),B(0,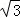 ,0),A(1,0,0),
,0),A(1,0,0),
设E(a,b,c),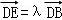 ,(0≤λ≤1),则(a,b,c﹣1)=λ(0,
,(0≤λ≤1),则(a,b,c﹣1)=λ(0,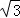 ,﹣1),解得E(0,
,﹣1),解得E(0,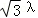 ,1﹣λ),
,1﹣λ),
∴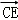 =(1,
=(1,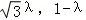 ),
),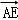 =(﹣1,
=(﹣1,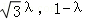 ),
),
∵AE⊥EC,∴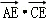 =﹣1+3λ2+(1﹣λ)2=0,
=﹣1+3λ2+(1﹣λ)2=0,
由λ∈[0,1],解得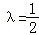 ,∴DE=BE,
,∴DE=BE,
∵四面体ABCE与四面体ACDE的高都是点A到平面BCD的高h,
∵DE=BE,∴S△DCE=S△BCE,
∴四面体ABCE与四面体ACDE的体积比为1.
【点评】本题考查线线垂直的证明,考查两个四面体的体积之比的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查数形结合思想、化归与转化思想,是中档题.
20.(12分)在直角坐标系xOy中,曲线y=x2+mx﹣2与x轴交于A、B两点,点C的坐标为(0,1),当m变化时,解答下列问题:
(1)能否出现AC⊥BC的情况?说明理由;
(2)证明过A、B、C三点的圆在y轴上截得的弦长为定值.
【考点】KJ:圆与圆锥曲线的综合.菁优网版权所有
【专题】34:方程思想;43:待定系数法;5B:直线与圆.
【分析】(1)设曲线y=x2+mx﹣2与x轴交于A(x1,0),B(x2,0),运用韦达定理,再假设AC⊥BC,运用直线的斜率之积为﹣1,即可判断是否存在这样的情况;
(2)设过A、B、C三点的圆的方程为x2+y2+Dx+Ey+F=0(D2+E2﹣4F>0),由题意可得D=m,F=﹣2,代入(0,1),可得E=1,再令x=0,即可得到圆在y轴的交点,进而得到弦长为定值.
【解答】解:(1)曲线y=x2+mx﹣2与x轴交于A、B两点,
可设A(x1,0),B(x2,0),
由韦达定理可得x1x2=﹣2,
若AC⊥BC,则kAC•kBC=﹣1,
即有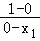 •
•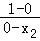 =﹣1,
=﹣1,
即为x1x2=﹣1这与x1x2=﹣2矛盾,
故不出现AC⊥BC的情况;
(2)证明:设过A、B、C三点的圆的方程为x2+y2+Dx+Ey+F=0(D2+E2﹣4F>0),
由题意可得y=0时,x2+Dx+F=0与x2+mx﹣2=0等价,
可得D=m,F=﹣2,
圆的方程即为x2+y2+mx+Ey﹣2=0,
由圆过C(0,1),可得0+1+0+E﹣2=0,可得E=1,
则圆的方程即为x2+y2+mx+y﹣2=0,
另解:设过A、B、C三点的圆在y轴上的交点为H(0,d),
则由相交弦定理可得|OA|•|OB|=|OC|•|OH|,
即有2=|OH|,
再令x=0,可得y2+y﹣2=0,
解得y=1或﹣2.
即有圆与y轴的交点为(0,1),(0,﹣2),
则过A、B、C三点的圆在y轴上截得的弦长为定值3.
【点评】本题考查直线与圆的方程的求法,注意运用韦达定理和直线的斜率公式,以及待定系数法,考查方程思想和化简整理的运算能力,属于中档题.
21.(12分)已知函数f(x)=lnx+ax2+(2a+1)x.
(1)讨论f(x)的单调性;
(2)当a<0时,证明f(x)≤﹣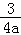 ﹣2.
﹣2.
【考点】6B:利用导数研究函数的单调性;6E:利用导数研究函数的最值.菁优网版权所有
【专题】11:计算题;32:分类讨论;48:分析法;53:导数的综合应用.
【分析】(1)题干求导可知f′(x)=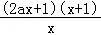 (x>0),分a=0、a>0、a<0三种情况讨论f′(x)与0的大小关系可得结论;
(x>0),分a=0、a>0、a<0三种情况讨论f′(x)与0的大小关系可得结论;
(2)通过(1)可知f(x)max=f(﹣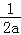 )=﹣1﹣ln2﹣
)=﹣1﹣ln2﹣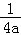 +ln(﹣
+ln(﹣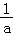 ),进而转化可知问题转化为证明:当t>0时﹣
),进而转化可知问题转化为证明:当t>0时﹣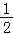 t+lnt≤﹣1+ln2.进而令g(t)=﹣
t+lnt≤﹣1+ln2.进而令g(t)=﹣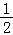 t+lnt,利用导数求出y=g(t)的最大值即可.
t+lnt,利用导数求出y=g(t)的最大值即可.
【解答】(1)解:因为f(x)=lnx+ax2+(2a+1)x,
求导f′(x)=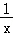 +2ax+(2a+1)=
+2ax+(2a+1)=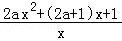 =
=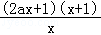 ,(x>0),
,(x>0),
①当a=0时,f′(x)=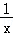 +1>0恒成立,此时y=f(x)在(0,+∞)上单调递增;
+1>0恒成立,此时y=f(x)在(0,+∞)上单调递增;
②当a>0,由于x>0,所以(2ax+1)(x+1)>0恒成立,此时y=f(x)在(0,+∞)上单调递增;
③当a<0时,令f′(x)=0,解得:x=﹣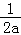 .
.
因为当x∈(0,﹣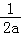 )f′(x)>0、当x∈(﹣
)f′(x)>0、当x∈(﹣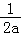 ,+∞)f′(x)<0,
,+∞)f′(x)<0,
所以y=f(x)在(0,﹣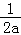 )上单调递增、在(﹣
)上单调递增、在(﹣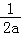 ,+∞)上单调递减.
,+∞)上单调递减.
综上可知:当a≥0时f(x)在(0,+∞)上单调递增,
当a<0时,f(x)在(0,﹣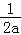 )上单调递增、在(﹣
)上单调递增、在(﹣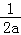 ,+∞)上单调递减;
,+∞)上单调递减;
(2)证明:由(1)可知:当a<0时f(x)在(0,﹣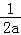 )上单调递增、在(﹣
)上单调递增、在(﹣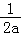 ,+∞)上单调递减,
,+∞)上单调递减,
所以当x=﹣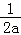 时函数y=f(x)取最大值f(x)max=f(﹣
时函数y=f(x)取最大值f(x)max=f(﹣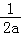 )=﹣1﹣ln2﹣
)=﹣1﹣ln2﹣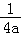 +ln(﹣
+ln(﹣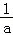 ).
).
从而要证f(x)≤﹣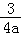 ﹣2,即证f(﹣
﹣2,即证f(﹣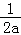 )≤﹣
)≤﹣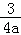 ﹣2,
﹣2,
即证﹣1﹣ln2﹣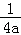 +ln(﹣
+ln(﹣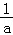 )≤﹣
)≤﹣ ﹣2,即证﹣
﹣2,即证﹣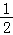 (﹣
(﹣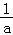 )+ln(﹣
)+ln(﹣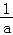 )≤﹣1+ln2.
)≤﹣1+ln2.
令t=﹣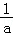 ,则t>0,问题转化为证明:﹣
,则t>0,问题转化为证明:﹣ t+lnt≤﹣1+ln2.…(*)
t+lnt≤﹣1+ln2.…(*)
令g(t)=﹣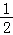 t+lnt,则g′(t)=﹣
t+lnt,则g′(t)=﹣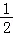 +
+ ,
,
令g′(t)=0可知t=2,则当0<t<2时g′(t)>0,当t>2时g′(t)<0,
所以y=g(t)在(0,2)上单调递增、在(2,+∞)上单调递减,
即g(t)≤g(2)=﹣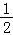 ×2+ln2=﹣1+ln2,即(*)式成立,
×2+ln2=﹣1+ln2,即(*)式成立,
所以当a<0时,f(x)≤﹣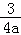 ﹣2成立.
﹣2成立.
【点评】本题考查利用导数研究函数的单调性,考查分类讨论的思想,考查转化能力,考查运算求解能力,注意解题方法的积累,属于中档题.
[选修4-4:坐标系与参数方程]
22.(10分)在直角坐标系xOy中,直线l1的参数方程为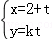 ,(t为参数),直线l2的参数方程为
,(t为参数),直线l2的参数方程为 ,(m为参数).设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
,(m为参数).设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
(1)写出C的普通方程;
(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ)﹣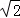 =0,M为l3与C的交点,求M的极径.
=0,M为l3与C的交点,求M的极径.
【考点】QH:参数方程化成普通方程.菁优网版权所有
【专题】34:方程思想;4Q:参数法;4R:转化法;5S:坐标系和参数方程.
【分析】解:(1)分别消掉参数t与m可得直线l1与直线l2的普通方程为y=k(x﹣2)①与x=﹣2+ky②;联立①②,消去k可得C的普通方程为x2﹣y2=4;
(2)将l3的极坐标方程为ρ(cosθ+sinθ)﹣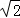 =0化为普通方程:x+y﹣
=0化为普通方程:x+y﹣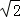 =0,再与曲线C的方程联立,可得
=0,再与曲线C的方程联立,可得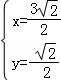 ,即可求得l3与C的交点M的极径为ρ=
,即可求得l3与C的交点M的极径为ρ=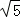 .
.
【解答】解:(1)∵直线l1的参数方程为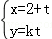 ,(t为参数),
,(t为参数),
∴消掉参数t得:直线l1的普通方程为:y=k(x﹣2)①;
又直线l2的参数方程为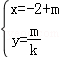 ,(m为参数),
,(m为参数),
同理可得,直线l2的普通方程为:x=﹣2+ky②;
联立①②,消去k得:x2﹣y2=4,即C的普通方程为x2﹣y2=4(x≠2且y≠0);
(2)∵l3的极坐标方程为ρ(cosθ+sinθ)﹣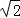 =0,
=0,
∴其普通方程为:x+y﹣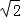 =0,
=0,
联立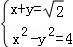 得:
得: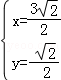 ,
,
∴ρ2=x2+y2=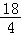 +
+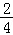 =5.
=5.
∴l3与C的交点M的极径为ρ=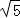 .
.
【点评】本题考查参数方程与极坐标方程化普通方程,考查函数与方程思想与等价转化思想的运用,属于中档题.
[选修4-5:不等式选讲]
23.已知函数f(x)=|x+1|﹣|x﹣2|.
(1)求不等式f(x)≥1的解集;
(2)若不等式f(x)≥x2﹣x+m的解集非空,求m的取值范围.
【考点】R4:绝对值三角不等式;R5:绝对值不等式的解法.菁优网版权所有
【专题】32:分类讨论;33:函数思想;4C:分类法;4R:转化法;51:函数的性质及应用;5T:不等式.
【分析】(1)由于f(x)=|x+1|﹣|x﹣2|=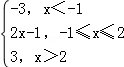 ,解不等式f(x)≥1可分﹣1≤x≤2与x>2两类讨论即可解得不等式f(x)≥1的解集;
,解不等式f(x)≥1可分﹣1≤x≤2与x>2两类讨论即可解得不等式f(x)≥1的解集;
(2)依题意可得m≤[f(x)﹣x2+x]max,设g(x)=f(x)﹣x2+x,分x≤1、﹣1<x<2、x≥2三类讨论,可求得g(x)max= ,从而可得m的取值范围.
,从而可得m的取值范围.
【解答】解:(1)∵f(x)=|x+1|﹣|x﹣2|=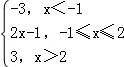 ,f(x)≥1,
,f(x)≥1,
∴当﹣1≤x≤2时,2x﹣1≥1,解得1≤x≤2;
当x>2时,3≥1恒成立,故x>2;
综上,不等式f(x)≥1的解集为{x|x≥1}.
(2)原式等价于存在x∈R使得f(x)﹣x2+x≥m成立,
即m≤[f(x)﹣x2+x]max,设g(x)=f(x)﹣x2+x.
由(1)知,g(x)=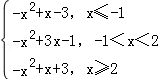 ,
,
当x≤﹣1时,g(x)=﹣x2+x﹣3,其开口向下,对称轴方程为x=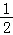 >﹣1,
>﹣1,
∴g(x)≤g(﹣1)=﹣1﹣1﹣3=﹣5;
当﹣1<x<2时,g(x)=﹣x2+3x﹣1,其开口向下,对称轴方程为x=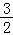 ∈(﹣1,2),
∈(﹣1,2),
∴g(x)≤g(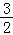 )=﹣
)=﹣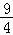 +
+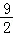 ﹣1=
﹣1=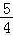 ;
;
当x≥2时,g(x)=﹣x2+x+3,其开口向下,对称轴方程为x=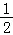 <2,
<2,
∴g(x)≤g(2)=﹣4+2+3=1;
综上,g(x)max=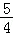 ,
,
∴m的取值范围为(﹣∞,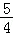 ].
].
【点评】本题考查绝对值不等式的解法,去掉绝对值符号是解决问题的关键,突出考查分类讨论思想与等价转化思想、函数与方程思想的综合运用,属于难题.

