2008年四川省高考数学试卷(理科)(含解析版)
2008年四川省高考数学试卷(理科)
一、选择题(共12小题,每小题5分,满分60分)
1.(5分)已知全集U={1,2,3,4,5},集合A={1,3},B={3,4,5},则集合∁U(A∩B)=( )
A.{3}B.{4,5} C.{3,4,5} D.{1,2,4,5}
2.(5分)复数2i(1+i)2=( )
A.﹣4B.4 C.﹣4i D.4i
3.(5分)(tanx+cotx)cos2x=( )
A.tanxB.sinx C.cosx D.cotx
4.(5分)直线y=3x绕原点逆时针旋转90°,再向右平移1个单位,所得到的直线为( )
A.B.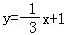 C.y=3x﹣3 D.
C.y=3x﹣3 D.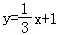
5.(5分)若0≤α≤2π,sinα>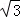 cosα,则α的取值范围是( )
cosα,则α的取值范围是( )
A.(,)B.(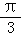 ,π) C.(
,π) C.(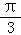 ,
,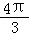 ) D.(
) D.(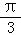 ,
,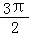 )
)
6.(5分)从甲、乙等10个同学中挑选4名参加某项公益活动,要求甲、乙中至少有1人参加,则不同的挑选方法共有( )
A.70种B.112种 C.140种 D.168种
7.(5分)已知等比数列{an}中,a2=1,则其前3项的和S3的取值范围是( )
A.(﹣∞,﹣1]B.(﹣∞,0)∪(1,+∞)
C.[3,+∞)D.(﹣∞,﹣1]∪[3,+∞)
8.(5分)设M,N是球心O的半径OP上的两点,且NP=MN=OM,分别过N,M,O作垂线于OP的面截球得三个圆,则这三个圆的面积之比为:( )
A.3,5,6B.3,6,8 C.5,7,9 D.5,8,9
9.(5分)设直线l⊂平面α,过平面α外一点A与l,α都成30°角的直线有且只有( )
A.1条B.2条 C.3条 D.4条
10.(5分)设f(x)=sin(ωx+φ),其中ω>0,则f(x)是偶函数的充要条件是( )
A.f(0)=1B.f(0)=0 C.f′(0)=1 D.f′(0)=0
11.(5分)设定义在R上的函数f(x)满足f(x)•f(x+2)=13,若f(1)=2,则f(99)=( )
A.13B.2 C.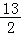 D.
D.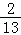
12.(5分)已知抛物线C:y2=8x的焦点为F,准线与x轴的交点为K,点A在C上且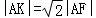 ,则△AFK的面积为( )
,则△AFK的面积为( )
A.4B.8 C.16 D.32
二、填空题(共4小题,每小题4分,满分16分)
13.(4分)(1+2x)3(1﹣x)4展开式中x2的系数为 .
14.(4分)已知直线l:x﹣y+4=0与圆C:(x﹣1)2+(y﹣1)2=2,则C上各点到l的距离的最小值为 .
15.(4分)已知正四棱柱的对角线的长为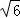 ,且对角线与底面所成角的余弦值为
,且对角线与底面所成角的余弦值为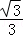 ,则该正四棱柱的体积等于 .
,则该正四棱柱的体积等于 .
16.(4分)设等差数列{an}的前n项和为Sn,若S4≥10,S5≤15,则a4的最大值为 .
三、解答题(共6小题,满分74分)
17.(12分)求函数y=7﹣4sinxcosx+4cos2x﹣4cos4x的最大值与最小值.
18.(12分)设进入某商场的每一位顾客购买甲种商品的概率为0.5,购买乙种商品的概率为0.6,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的.
(Ⅰ)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(Ⅱ)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(Ⅲ)记ξ表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求ξ的分布列及期望.
19.(12分)如,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,BC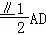 ,BE
,BE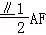
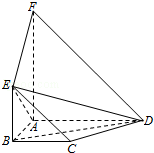
(Ⅰ)证明:C,D,F,E四点共面;
(Ⅱ)设AB=BC=BE,求二面角A﹣ED﹣B的大小.
20.(12分)设数列{an}的前n项和为Sn,已知ban﹣2n=(b﹣1)Sn
(Ⅰ)证明:当b=2时,{an﹣n•2n﹣1}是等比数列;
(Ⅱ)求{an}的通项公式.
21.(12分)设椭圆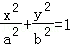 ,({a>b>0})的左右焦点分别为F1,F2,离心率
,({a>b>0})的左右焦点分别为F1,F2,离心率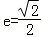 ,右准线为l,M,N是l上的两个动点,
,右准线为l,M,N是l上的两个动点,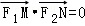
(Ⅰ)若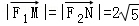 ,求a,b的值;
,求a,b的值;
(Ⅱ)证明:当|MN|取最小值时,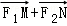 与
与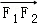 共线.
共线.
22.(14分)已知x=3是函数f(x)=aln(1+x)+x2﹣10x的一个极值点.
(Ⅰ)求a;
(Ⅱ)求函数f(x)的单调区间;
(Ⅲ)若直线y=b与函数y=f(x)的图象有3个交点,求b的取值范围.
2008年四川省高考数学试卷(理科)
参考答案与试题解析
一、选择题(共12小题,每小题5分,满分60分)
1.(5分)已知全集U={1,2,3,4,5},集合A={1,3},B={3,4,5},则集合∁U(A∩B)=( )
A.{3}B.{4,5} C.{3,4,5} D.{1,2,4,5}
【考点】1H:交、并、补集的混合运算.菁优网版权所有
【分析】根据交集的含义求A∩B、再根据补集的含义求解.
【解答】解:A={1,3},B={3,4,5}⇒A∩B={3};
所以CU(A∩B)={1,2,4,5},
故选:D.
【点评】本题考查集合的基本运算,较简单.
2.(5分)复数2i(1+i)2=( )
A.﹣4B.4 C.﹣4i D.4i
【考点】A5:复数的运算.菁优网版权所有
【分析】先算(1+i)2,再算乘2i,化简即可.
【解答】解:∵2i(1+i)2=2i(1+2i﹣1)=2i×2i=4i2=﹣4
故选:A.
【点评】此题考查复数的运算,乘法公式,以及注意i2=﹣1;是基础题.
3.(5分)(tanx+cotx)cos2x=( )
A.tanxB.sinx C.cosx D.cotx
【考点】GG:同角三角函数间的基本关系.菁优网版权所有
【分析】此题重点考查各三角函数的关系,切化弦,约分整理,凑出同一角的正弦和余弦的平方和,再约分化简.
【解答】解:∵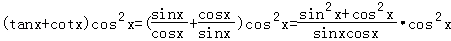
=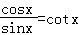
故选:D.
【点评】将不同的角化为同角;将不同名的函数化为同名函数,以减少函数的种类;当式中有正切、余切、正割、余割时,通常把式子化成含有正弦与余弦的式子,即所谓“切割化弦”.
4.(5分)直线y=3x绕原点逆时针旋转90°,再向右平移1个单位,所得到的直线为( )
A.B.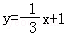 C.y=3x﹣3 D.
C.y=3x﹣3 D.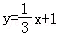
【考点】IA:两条直线垂直与倾斜角、斜率的关系.菁优网版权所有
【分析】先利用两直线垂直写出第一次方程,再由平移写出第二次方程.
【解答】解:∵直线y=3x绕原点逆时针旋转90°
∴两直线互相垂直
则该直线为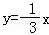 ,
,
那么将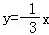 向右平移1个单位得
向右平移1个单位得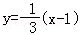 ,即
,即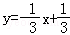
故选:A.
【点评】本题主要考查互相垂直的直线关系,同时考查直线平移问题.
5.(5分)若0≤α≤2π,sinα>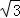 cosα,则α的取值范围是( )
cosα,则α的取值范围是( )
A.(,)B.(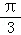 ,π) C.(
,π) C.(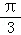 ,
,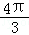 ) D.(
) D.(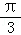 ,
,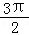 )
)
【考点】GA:三角函数线;HF:正切函数的单调性和周期性.菁优网版权所有
【专题】11:计算题.
【分析】通过对sinα>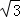 cosα等价变形,利用辅助角公式化为正弦,利用正弦函数的性质即可得到答案.
cosα等价变形,利用辅助角公式化为正弦,利用正弦函数的性质即可得到答案.
【解答】解:∵0≤α≤2π,sinα>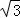 cosα,
cosα,
∴sinα﹣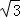 cosα=2sin(α﹣
cosα=2sin(α﹣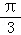 )>0,
)>0,
∵0≤α≤2π,
∴﹣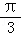 ≤α﹣
≤α﹣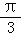 ≤
≤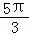 ,
,
∵2sin(α﹣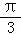 )>0,
)>0,
∴0<α﹣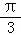 <π,
<π,
∴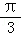 <α<
<α<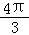 .
.
故选:C.
【点评】本题考查辅助角公式的应用,考查正弦函数的性质,将sinα>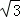 cosα等价变形是难点,也是易错点,属于中档题.
cosα等价变形是难点,也是易错点,属于中档题.
6.(5分)从甲、乙等10个同学中挑选4名参加某项公益活动,要求甲、乙中至少有1人参加,则不同的挑选方法共有( )
A.70种B.112种 C.140种 D.168种
【考点】D5:组合及组合数公式.菁优网版权所有
【专题】11:计算题.
【分析】根据题意,分析可得,甲、乙中至少有1人参加的情况数目等于从10个同学中挑选4名参加公益活动挑选方法数减去从甲、乙之外的8个同学中挑选4名参加公益活动的挑选方法数,分别求出其情况数目,计算可得答案.
【解答】解:∵从10个同学中挑选4名参加某项公益活动有C104种不同挑选方法;
从甲、乙之外的8个同学中挑选4名参加某项公益活动有C84种不同挑选方法;
∴甲、乙中至少有1人参加,则不同的挑选方法共有C104﹣C84=210﹣70=140种不同挑选方法,
故选:C.
【点评】此题重点考查组合的意义和组合数公式,本题中,要注意找准切入点,从反面下手,方法较简单.
7.(5分)已知等比数列{an}中,a2=1,则其前3项的和S3的取值范围是( )
A.(﹣∞,﹣1]B.(﹣∞,0)∪(1,+∞)
C.[3,+∞)D.(﹣∞,﹣1]∪[3,+∞)
【考点】89:等比数列的前n项和.菁优网版权所有
【分析】首先由等比数列的通项入手表示出S3(即q的代数式),然后根据q的正负性进行分类,最后利用均值不等式求出S3的范围.
【解答】解:∵等比数列{an}中,a2=1
∴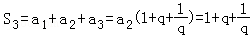
∴当公比q>0时,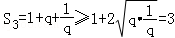 ;
;
当公比q<0时,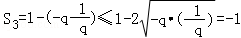 .
.
∴S3∈(﹣∞,﹣1]∪[3,+∞).
故选:D.
【点评】本题考查等比数列前n项和的意义、等比数列的通项公式及均值不等式的应用.
8.(5分)设M,N是球心O的半径OP上的两点,且NP=MN=OM,分别过N,M,O作垂线于OP的面截球得三个圆,则这三个圆的面积之比为:( )
A.3,5,6B.3,6,8 C.5,7,9 D.5,8,9
【考点】L*:球面距离及相关计算.菁优网版权所有
【专题】11:计算题.
【分析】先求截面圆的半径,然后求出三个圆的面积的比.
【解答】解:设分别过N,M,O作垂线于OP的面截球得三个圆的半径为r1,r2,r3,球半径为R,则: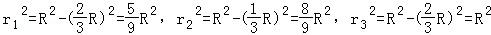
∴r12:r22:r32=5:8:9∴这三个圆的面积之比为:5,8,9
故选:D.
【点评】此题重点考查球中截面圆半径,球半径之间的关系;考查空间想象能力,利用勾股定理的计算能力.
9.(5分)设直线l⊂平面α,过平面α外一点A与l,α都成30°角的直线有且只有( )
A.1条B.2条 C.3条 D.4条
【考点】LP:空间中直线与平面之间的位置关系.菁优网版权所有
【分析】利用圆锥的母线与底面所成的交角不变画图,即可得到结果.
【解答】解:如图,和α成30°角的直线一定是以A为顶点的圆锥的母线所在直线,当∠ABC=∠ACB=30°,直线AC,AB都满足条件
故选:B.
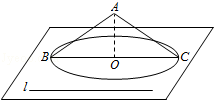
【点评】此题重点考查线线角,线面角的关系,以及空间想象能力,图形的对称性;
数形结合,重视空间想象能力和图形的对称性;
10.(5分)设f(x)=sin(ωx+φ),其中ω>0,则f(x)是偶函数的充要条件是( )
A.f(0)=1B.f(0)=0 C.f′(0)=1 D.f′(0)=0
【考点】HJ:函数y=Asin(ωx+φ)的图象变换.菁优网版权所有
【专题】11:计算题.
【分析】当f(x)=sin(ωx+φ)是偶函数时,f(0)一定是函数的最值,从而得到x=0必是f(x)的极值点,即f′(0)=0,因而得到答案.
【解答】解:∵f(x)=sin(ωx+φ)是偶函数
∴由函数f(x)=sin(ωx+φ)图象特征可知x=0必是f(x)的极值点,
∴f′(0)=0
故选:D.
【点评】此题重点考查正弦型函数的图象特征,函数的奇偶性,函数的极值点与函数导数的关系.
11.(5分)设定义在R上的函数f(x)满足f(x)•f(x+2)=13,若f(1)=2,则f(99)=( )
A.13B.2 C.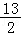 D.
D.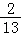
【考点】3T:函数的值.菁优网版权所有
【专题】16:压轴题.
【分析】根据f(1)=2,f(x)•f(x+2)=13先求出f(3)=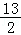 ,再由f(3)求出f(5),依次求出f(7)、f(9)观察规律可求出f(x)的解析式,最终得到答案.
,再由f(3)求出f(5),依次求出f(7)、f(9)观察规律可求出f(x)的解析式,最终得到答案.
【解答】解:∵f(x)•f(x+2)=13且f(1)=2
∴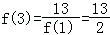 ,
,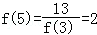 ,
,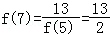 ,
,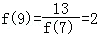 ,
,
∴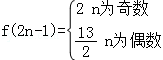 ,
,
∴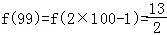
故选:C.
【点评】此题重点考查递推关系下的函数求值;此类题的解决方法一般是求出函数解析式后代值,或者得到函数的周期性求解.
12.(5分)已知抛物线C:y2=8x的焦点为F,准线与x轴的交点为K,点A在C上且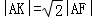 ,则△AFK的面积为( )
,则△AFK的面积为( )
A.4B.8 C.16 D.32
【考点】K8:抛物线的性质.菁优网版权所有
【专题】11:计算题;16:压轴题.
【分析】根据抛物线的方程可知焦点坐标和准线方程,进而可求得K的坐标,设A(x0,y0),过A点向准线作垂线AB,则B(﹣2,y0),根据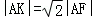 及AF=AB=x0﹣(﹣2)=x0+2,进而可求得A点坐标,进而求得△AFK的面积.
及AF=AB=x0﹣(﹣2)=x0+2,进而可求得A点坐标,进而求得△AFK的面积.
【解答】解:∵抛物线C:y2=8x的焦点为F(2,0),准线为x=﹣2
∴K(﹣2,0)
设A(x0,y0),过A点向准线作垂线AB,则B(﹣2,y0)
∵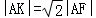 ,又AF=AB=x0﹣(﹣2)=x0+2
,又AF=AB=x0﹣(﹣2)=x0+2
∴由BK2=AK2﹣AB2得y02=(x0+2)2,即8x0=(x0+2)2,解得A(2,±4)
∴△AFK的面积为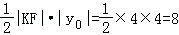
故选:B.
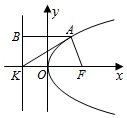
【点评】本题抛物线的性质,由题意准确画出图象,利用离心率转化位置,在△ABK中集中条件求出x0是关键;
二、填空题(共4小题,每小题4分,满分16分)
13.(4分)(1+2x)3(1﹣x)4展开式中x2的系数为 ﹣6 .
【考点】DA:二项式定理.菁优网版权所有
【专题】11:计算题.
【分析】利用乘法原理找展开式中的含x2项的系数,注意两个展开式的结合分析,即分别为第一个展开式的常数项和第二个展开式的x2的乘积、第一个展开式的含x项和第二个展开式的x项的乘积、第一个展开式的x2的项和第二个展开式的常数项的乘积之和从而求出答案.
【解答】解:∵(1+2x)3(1﹣x)4展开式中x2项为
C3013(2x)0•C4212(﹣x)2+C3112(2x)1•C4113(﹣x)1+C3212(2x)2•C4014(﹣x)0
∴所求系数为C30•C42+C31•2•C41(﹣1)+C32•22•C4014=6﹣24+12=﹣6.
故答案为:﹣6.
【点评】此题重点考查二项展开式中指定项的系数,以及组合思想,重在找寻这些项的来源.
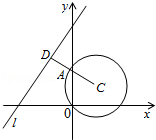
14.(4分)已知直线l:x﹣y+4=0与圆C:(x﹣1)2+(y﹣1)2=2,则C上各点到l的距离的最小值为 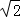 .
.
【考点】IT:点到直线的距离公式;J9:直线与圆的位置关系.菁优网版权所有
【专题】31:数形结合.
【分析】如图过点C作出CD与直线l垂直,垂足为D,与圆C交于点A,则AD为所求;求AD的方法是:由圆的方程找出圆心坐标与圆的半径,然后利用点到直线的距离公式求出圆心到直线l的距离d,利用d减去圆的半径r即为圆上的点到直线l的距离的最小值.
【解答】解:如图可知:过圆心作直线l:x﹣y+4=0的垂线,则AD长即为所求;
∵圆C:(x﹣1)2+(y﹣1)2=2的圆心为C(1,1),半径为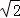 ,
,
点C到直线l:x﹣y+4=0的距离为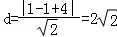 ,
,
∴AD=CD﹣AC=2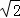 ﹣
﹣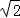 =
=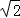 ,
,
故C上各点到l的距离的最小值为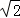 .
.
故答案为: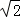
【点评】此题重点考查圆的标准方程和点到直线的距离.本题的突破点是数形结合,使用点C到直线l的距离距离公式.
15.(4分)已知正四棱柱的对角线的长为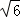 ,且对角线与底面所成角的余弦值为
,且对角线与底面所成角的余弦值为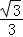 ,则该正四棱柱的体积等于 2 .
,则该正四棱柱的体积等于 2 .
【考点】LF:棱柱、棱锥、棱台的体积.菁优网版权所有
【专题】11:计算题;13:作图题;16:压轴题.
【分析】由题意画出图形,求出高,底面边长,然后求出该正四棱柱的体积.
【解答】解::如图可知:∵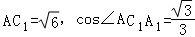
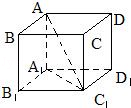
∴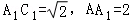 ∴正四棱柱的体积等于
∴正四棱柱的体积等于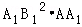 =2
=2
故答案为:2
【点评】此题重点考查线面角,解直角三角形,以及求正四面题的体积;考查数形结合,重视在立体几何中解直角三角形,熟记有关公式.
16.(4分)设等差数列{an}的前n项和为Sn,若S4≥10,S5≤15,则a4的最大值为 4 .
【考点】83:等差数列的性质;85:等差数列的前n项和.菁优网版权所有
【专题】16:压轴题.
【分析】利用等差数列的前n项和公式变形为不等式,再利用消元思想确定d或a1的范围,a4用d或a1表示,再用不等式的性质求得其范围.
【解答】解:∵等差数列{an}的前n项和为Sn,且S4≥10,S5≤15,
∴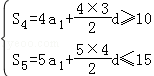 ,
,
即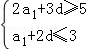
∴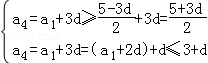
∴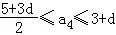 ,5+3d≤6+2d,d≤1
,5+3d≤6+2d,d≤1
∴a4≤3+d≤3+1=4故a4的最大值为4,
故答案为:4.
【点评】此题重点考查等差数列的通项公式,前n项和公式,以及不等式的变形求范围;
三、解答题(共6小题,满分74分)
17.(12分)求函数y=7﹣4sinxcosx+4cos2x﹣4cos4x的最大值与最小值.
【考点】HW:三角函数的最值.菁优网版权所有
【专题】11:计算题.
【分析】利用二倍角的正弦函数公式及同角三角函数间的基本关系化简y的解析式后,再利用配方法把y变为完全平方式即y=(1﹣sin2x)2+6,可设z═(u﹣1)2+6,u=sin2x,因为sin2x的范围为[﹣1,1],根据u属于[﹣1,1]时,二次函数为递减函数,利用二次函数求最值的方法求出z的最值即可得到y的最大和最小值.
【解答】解:y=7﹣4sinxcosx+4cos2x﹣4cos4x=7﹣2sin2x+4cos2x(1﹣cos2x)=7﹣2sin2x+4cos2xsin2x=7﹣2sin2x+sin22x=(1﹣sin2x)2+6
由于函数z=(u﹣1)2+6在[﹣1,1]中的最大值为zmax=(﹣1﹣1)2+6=10
最小值为zmin=(1﹣1)2+6=6
故当sin2x=﹣1时y取得最大值10,当sin2x=1时y取得最小值6
【点评】此题重点考查三角函数基本公式的变形,配方法,符合函数的值域及最值;本题的突破点是利用倍角公式降幂,利用配方变为复合函数,重视复合函数中间变量的范围是关键.
18.(12分)设进入某商场的每一位顾客购买甲种商品的概率为0.5,购买乙种商品的概率为0.6,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的.
(Ⅰ)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(Ⅱ)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(Ⅲ)记ξ表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求ξ的分布列及期望.
【考点】C8:相互独立事件和相互独立事件的概率乘法公式;CG:离散型随机变量及其分布列;CH:离散型随机变量的期望与方差.菁优网版权所有
【专题】11:计算题.
【分析】(1)进入商场的1位顾客购买甲、乙两种商品中的一种,包括两种情况:即进入商场的1位顾客购买甲种商品不购买乙种商品,进入商场的1位顾客购买乙种商品不购买甲种商品,分析后代入相互独立事件的概率乘法公式即可得到结论.
(2)进入商场的1位顾客至少购买甲、乙两种商品中的一种的对立事件为,该顾客即不习甲商品也不购买乙商品,我们可以利用对立事件概率减法公式求解.
(3)由(1)、(2)的结论,我们列出ξ的分布列,计算后代入期望公式即可得到数学期望.
【解答】解:记A表示事件:进入商场的1位顾客购买甲种商品,
记B表示事件:进入商场的1位顾客购买乙种商品,
记C表示事件:进入商场的1位顾客购买甲、乙两种商品中的一种,
记D表示事件:进入商场的1位顾客至少购买甲、乙两种商品中的一种,
(Ⅰ)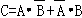
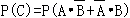
=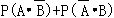
=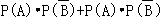
=0.5×0.4+0.5×0.6=0.5
(Ⅱ)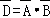
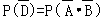
=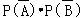
=0.5×0.4
=0.2
∴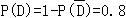
(Ⅲ)ξ~B(3,0.8),
故ξ的分布列P(ξ=0)=0.23=0.008
P(ξ=1)=C31×0.8×0.22=0.096
P(ξ=2)=C32×0.82×0.2=0.384
P(ξ=3)=0.83=0.512
所以Eξ=3×0.8=2.4
【点评】此题重点考查相互独立事件的概率计算,以及求随机变量的概率分布列和数学期望;突破口:分清相互独立事件的概率求法,对于“至少”常从反面入手常可起到简化的作用;
19.(12分)如,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,BC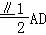 ,BE
,BE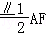
(Ⅰ)证明:C,D,F,E四点共面;
(Ⅱ)设AB=BC=BE,求二面角A﹣ED﹣B的大小.
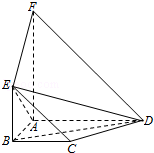
【考点】LJ:平面的基本性质及推论;MJ:二面角的平面角及求法.菁优网版权所有
【专题】11:计算题;14:证明题.
【分析】(Ⅰ)延长DC交AB的延长线于点G,延长FE交AB的延长线于G′,根据比例关系可证得G与G′重合,准确推理,得到直线CD、EF相交于点G,即C,D,F,E四点共面.
(Ⅱ)取AE中点M,作MN⊥DE,垂足为N,连接BN,由三垂线定理知BN⊥ED,根据二面角平面角的定义可知∠BMN为二面角A﹣ED﹣B的平面角,在三角形BMN中求出此角即可.
【解答】解:(Ⅰ)延长DC交AB的延长线于点G,由BC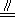
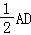 得
得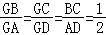
延长FE交AB的延长线于G′
同理可得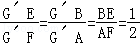
故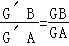 ,即G与G′重合
,即G与G′重合
因此直线CD、EF相交于点G,即C,D,F,E四点共面.
(Ⅱ)设AB=1,则BC=BE=1,AD=2
取AE中点M,则BM⊥AE,又由已知得,AD⊥平面ABEF
故AD⊥BM,BM与平面ADE内两相交直线AD、AE都垂直.
所以BM⊥平面ADE,作MN⊥DE,垂足为N,连接BN
由三垂线定理知BN⊥ED,∠BMN为二面角A﹣ED﹣B的平面角.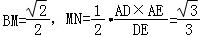
故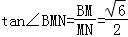
所以二面角A﹣ED﹣B的大小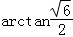
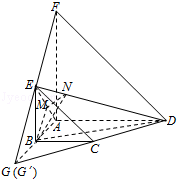
【点评】此题重点考查立体几何中四点共面问题和求二面角的问题,考查空间想象能力,几何逻辑推理能力,以及计算能力;突破:熟悉几何公理化体系,准确推理,注意书写格式是顺利进行求解的关键.
20.(12分)设数列{an}的前n项和为Sn,已知ban﹣2n=(b﹣1)Sn
(Ⅰ)证明:当b=2时,{an﹣n•2n﹣1}是等比数列;
(Ⅱ)求{an}的通项公式.
【考点】8B:数列的应用.菁优网版权所有
【专题】11:计算题;14:证明题.
【分析】(Ⅰ)当b=2时,由题设条件知an+1=2an+2n.由此可知an+1﹣(n+1)•2n=2an+2n﹣(n+1)•2n=2(an﹣n•2n﹣1),所以{an﹣n•2n﹣1}是首项为1,公比为2的等比数列.
(Ⅱ)当b=2时,由题设条件知an=(n+1)2n﹣1;当b≠2时,由题意得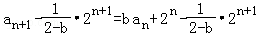 =
=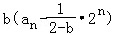 ,由此能够导出{an}的通项公式.
,由此能够导出{an}的通项公式.
【解答】解:(Ⅰ)当b=2时,由题意知2a1﹣2=a1,解得a1=2,
且ban﹣2n=(b﹣1)Sn
ban+1﹣2n+1=(b﹣1)Sn+1
两式相减得b(an+1﹣an)﹣2n=(b﹣1)an+1
即an+1=ban+2n①
当b=2时,由①知an+1=2an+2n
于是an+1﹣(n+1)•2n=2an+2n﹣(n+1)•2n=2(an﹣n•2n﹣1)
又a1﹣1•20=1≠0,所以{an﹣n•2n﹣1}是首项为1,公比为2的等比数列.
(Ⅱ)当b=2时,由(Ⅰ)知an﹣n•2n﹣1=2n﹣1,
即an=(n+1)2n﹣1
当b≠2时,由①得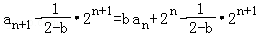
=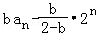 =
=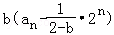
因此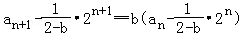 =
=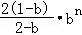
即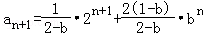
所以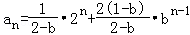 .
.
【点评】此题重点考查数列的递推公式,利用递推公式求数列的通项公式,同时考查分类讨论思想;推移脚标两式相减是解决含有Sn的递推公式的重要手段,使其转化为不含Sn的递推公式,从而针对性的解决;在由递推公式求通项公式是重视首项是否可以吸收是易错点,同时重视分类讨论,做到条理清晰是关键.
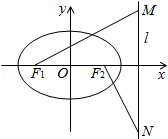
21.(12分)设椭圆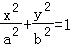 ,({a>b>0})的左右焦点分别为F1,F2,离心率
,({a>b>0})的左右焦点分别为F1,F2,离心率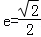 ,右准线为l,M,N是l上的两个动点,
,右准线为l,M,N是l上的两个动点,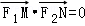
(Ⅰ)若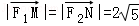 ,求a,b的值;
,求a,b的值;
(Ⅱ)证明:当|MN|取最小值时,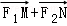 与
与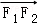 共线.
共线.
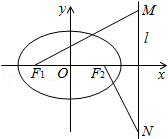
【考点】K4:椭圆的性质.菁优网版权所有
【专题】11:计算题;16:压轴题.
【分析】(Ⅰ)设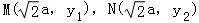 ,根据题意由
,根据题意由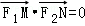 得
得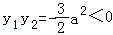 ,由
,由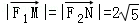 ,得
,得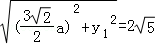 ,
,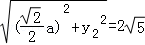 ,由此可以求出a,b的值.
,由此可以求出a,b的值.
(Ⅱ)|MN|2=(y1﹣y2)2=y12+y22﹣2y1y2≥﹣2y1y2﹣2y1y2=﹣4y1y2=6a2.当且仅当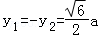 或
或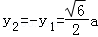 时,|MN|取最小值
时,|MN|取最小值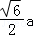 ,由能够推导出
,由能够推导出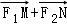 与
与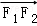 共线.
共线.
【解答】解:由a2﹣b2=c2与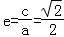 ,得a2=2b2,
,得a2=2b2,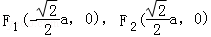 ,l的方程为
,l的方程为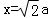
设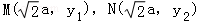
则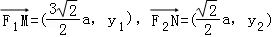
由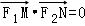 得
得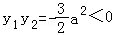 ①
①
(Ⅰ)由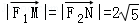 ,得
,得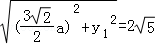 ②
②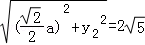 ③
③
由①、②、③三式,消去y1,y2,并求得a2=4
故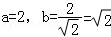
(Ⅱ)证明:|MN|2=(y1﹣y2)2=y12+y22﹣2y1y2≥﹣2y1y2﹣2y1y2=﹣4y1y2=6a2
当且仅当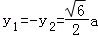 或
或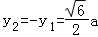 时,|MN|取最小值
时,|MN|取最小值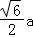
此时,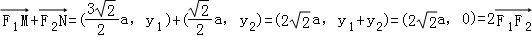
故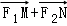 与
与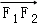 共线.
共线.
【点评】此题重点考查椭圆中的基本量的关系,进而求椭圆待定常数,考查向量的综合应用;熟悉椭圆各基本量间的关系,数形结合,熟练地进行向量的坐标运算,设而不求消元的思想在圆锥曲线问题中的灵活应用.
22.(14分)已知x=3是函数f(x)=aln(1+x)+x2﹣10x的一个极值点.
(Ⅰ)求a;
(Ⅱ)求函数f(x)的单调区间;
(Ⅲ)若直线y=b与函数y=f(x)的图象有3个交点,求b的取值范围.
【考点】6B:利用导数研究函数的单调性;6C:函数在某点取得极值的条件.菁优网版权所有
【专题】11:计算题;16:压轴题;44:数形结合法.
【分析】(Ⅰ)先求导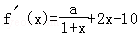 ,再由x=3是函数f(x)=aln(1+x)+x2﹣10x的一个极值点即
,再由x=3是函数f(x)=aln(1+x)+x2﹣10x的一个极值点即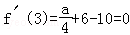 求解.
求解.
(Ⅱ)由(Ⅰ)确定f(x)=16ln(1+x)+x2﹣10x,x∈(﹣1,+∞),再由f′(x)>0和f′(x)<0求得单调区间.
(Ⅲ)由(Ⅱ)知,f(x)在(﹣1,1)内单调增加,在(1,3)内单调减少,在(3,+∞)上单调增加,且当x=1或x=3时,f′(x)=0,可得f(x)的极大值为f(1),极小值为f(3),再由直线y=b与函数y=f(x)的图象有3个交点则须有f(3)<b<f(1)求解,因此,b的取值范围为(32ln2﹣21,16ln2﹣9).
【解答】解:(Ⅰ)因为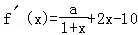
所以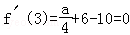
因此a=16
(Ⅱ)由(Ⅰ)知,f(x)=16ln(1+x)+x2﹣10x,x∈(﹣1,+∞),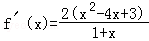
当x∈(﹣1,1)∪(3,+∞)时,f′(x)>0
当x∈(1,3)时,f′(x)<0
所以f(x)的单调增区间是(﹣1,1),(3,+∞),f(x)的单调减区间是(1,3)
(Ⅲ)由(Ⅱ)知,f(x)在(﹣1,1)内单调增加,
在(1,3)内单调减少,在(3,+∞)上单调增加,且当x=1或x=3时,f′(x)=0
所以f(x)的极大值为f(1)=16ln2﹣9,极小值为f(3)=32ln2﹣21
因此f(16)>162﹣10×16>16ln2﹣9=f(1),f(e﹣2﹣1)<﹣32+11=﹣21<f(3)
所以在f(x)的三个单调区间(﹣1,1),(1,3),(3,+∞)直线y=b有y=f(x)的图象各有一个交点,当且仅当f(3)<b<f(1)
因此,b的取值范围为(32ln2﹣21,16ln2﹣9).
【点评】此题重点考查利用求导研究函数的单调性,最值问题,函数根的问题;熟悉函数的求导公式,理解求导在函数最值中的研究方法是解题的关键,数形结合理解函数的取值范围.


