2016年四川省高考数学试卷(文科)(含解析版)
2016年四川省高考数学试卷(文科)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一个是符合题目要求的.
1.(5分)设i为虚数单位,则复数(1+i)2=( )
A.0B.2 C.2i D.2+2i
2.(5分)设集合A={x|1≤x≤5},Z为整数集,则集合A∩Z中元素的个数是( )
A.6B.5 C.4 D.3
3.(5分)抛物线y2=4x的焦点坐标是( )
A.(0,2)B.(0,1) C.(2,0) D.(1,0)
4.(5分)为了得到函数y=sin(x+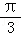 )的图象,只需把函数y=sinx的图象上所有的点( )
)的图象,只需把函数y=sinx的图象上所有的点( )
A.向左平行移动个单位长度B.向右平行移动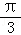 个单位长度
个单位长度
C.向上平行移动个单位长度D.向下平行移动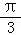 个单位长度
个单位长度
5.(5分)设p:实数x,y满足x>1且y>1,q:实数x,y满足x+y>2,则p是q的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
6.(5分)已知a为函数f(x)=x3﹣12x的极小值点,则a=( )
A.﹣4B.﹣2 C.4 D.2
7.(5分)某公司为激励创新,计划逐年加大研发资金投入.若该公司2015年全年投入研发资金130万元,在此基础上,每年投入的研发资金比上一年增长12%,则该公司全年投入的研发资金开始超过200万元的年份是( )
(参考数据:lg1.12=0.05,lg1.3=0.11,lg2=0.30)
A.2018年B.2019年 C.2020年 D.2021年
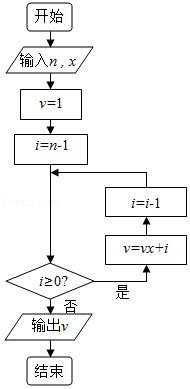
8.(5分)秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求多项式值的一个实例,若输入n,x的值分别为3,2,则输出v的值为( )
A.35B.20 C.18 D.9
9.(5分)已知正三角形ABC的边长为2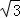 ,平面ABC内的动点P,M满足|
,平面ABC内的动点P,M满足|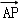 |=1,
|=1,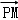 =
=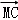 ,则|
,则|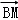 |2的最大值是( )
|2的最大值是( )
A.B.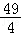 C.
C.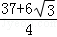 D.
D.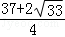
10.(5分)设直线l1,l2分别是函数f(x)=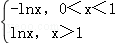 图象上点P1,P2处的切线,l1与l2垂直相交于点P,且l1,l2分别与y轴相交于点A,B,则△PAB的面积的取值范围是( )
图象上点P1,P2处的切线,l1与l2垂直相交于点P,且l1,l2分别与y轴相交于点A,B,则△PAB的面积的取值范围是( )
A.(0,1)B.(0,2) C.(0,+∞) D.(1,+∞)
二、填空题:本大题共5小题,每小题5分,共25分.
11.(5分)sin750°= .
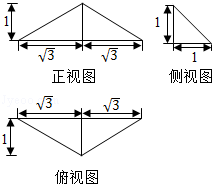
12.(5分)已知某三棱锥的三视图如图所示,则该三棱锥的体积是 .
13.(5分)从2,3,8,9中任取两个不同的数字,分别记为a,b,则logab为整数的概率是 .
14.(5分)若函数f(x)是定义R上的周期为2的奇函数,当0<x<1时,f(x)=4x,则f(﹣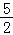 )+f(2)= .
)+f(2)= .
15.(5分)在平面直角坐标系中,当P(x,y)不是原点时,定义P的“伴随点”为P′(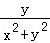 ,
,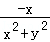 ),当P是原点时,定义“伴随点”为它自身,现有下列命题:
),当P是原点时,定义“伴随点”为它自身,现有下列命题:
①若点A的“伴随点”是点A′,则点A′的“伴随点”是点A.
②单元圆上的“伴随点”还在单位圆上.
③若两点关于x轴对称,则他们的“伴随点”关于y轴对称
④若三点在同一条直线上,则他们的“伴随点”一定共线.
其中的真命题是 .
三、解答题(共6小题,满分75分)
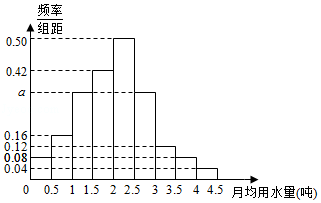
16.(12分)我国是世界上严重缺水的国家.某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨).将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(Ⅰ)求直方图中a的值;
(Ⅱ)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(Ⅲ)估计居民月均水量的中位数.
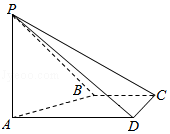
17.(12分)如图,在四棱锥P﹣ABCD中,PA⊥CD,AD∥BC,∠ADC=∠PAB=90°,BC=CD=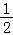 AD.
AD.
(Ⅰ)在平面PAD内找一点M,使得直线CM∥平面PAB,并说明理由;
(Ⅱ)证明:平面PAB⊥平面PBD.
18.(12分)在△ABC中,角A,B,C所对的边分别是a,b,c,且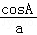 +
+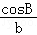 =
=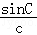 .
.
(Ⅰ)证明:sinAsinB=sinC;
(Ⅱ)若b2+c2﹣a2=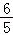 bc,求tanB.
bc,求tanB.
19.(12分)已知数列{an}的首项为1,Sn为数列{an}的前n项和,Sn+1=qSn+1,其中q>0,n∈N+
(Ⅰ)若a2,a3,a2+a3成等差数列,求数列{an}的通项公式;
(Ⅱ)设双曲线x2﹣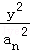 =1的离心率为en,且e2=2,求e12+e22+…+en2.
=1的离心率为en,且e2=2,求e12+e22+…+en2.
20.(13分)已知椭圆E: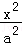 +
+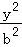 =1(a>b>0)的一个焦点与短轴的两个端点是正三角形的三个顶点,点P(
=1(a>b>0)的一个焦点与短轴的两个端点是正三角形的三个顶点,点P(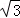 ,
,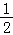 )在椭圆E上.
)在椭圆E上.
(Ⅰ)求椭圆E的方程;
(Ⅱ)设不过原点O且斜率为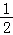 的直线l与椭圆E交于不同的两点A,B,线段AB的中点为M,直线OM与椭圆E交于C,D,证明:|MA|•|MB|=|MC|•|MD|
的直线l与椭圆E交于不同的两点A,B,线段AB的中点为M,直线OM与椭圆E交于C,D,证明:|MA|•|MB|=|MC|•|MD|
21.(14分)设函数f(x)=ax2﹣a﹣lnx,g(x)=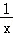 ﹣
﹣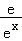 ,其中a∈R,e=2.718…为自然对数的底数.
,其中a∈R,e=2.718…为自然对数的底数.
(1)讨论f(x)的单调性;
(2)证明:当x>1时,g(x)>0;
(3)确定a的所有可能取值,使得f(x)>g(x)在区间(1,+∞)内恒成立.
2016年四川省高考数学试卷(文科)
参考答案与试题解析
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一个是符合题目要求的.
1.(5分)设i为虚数单位,则复数(1+i)2=( )
A.0B.2 C.2i D.2+2i
【考点】A5:复数的运算.菁优网版权所有
【专题】35:转化思想;49:综合法;5N:数系的扩充和复数.
【分析】利用复数的运算法则即可得出.
【解答】解:(1+i)2=1+i2+2i=1﹣1+2i=2i,
故选:C.
【点评】本题考查了复数的运算法则,考查了推理能力与计算能力,属于基础题.
2.(5分)设集合A={x|1≤x≤5},Z为整数集,则集合A∩Z中元素的个数是( )
A.6B.5 C.4 D.3
【考点】1E:交集及其运算.菁优网版权所有
【专题】35:转化思想;59:不等式的解法及应用;5J:集合.
【分析】利用交集的运算性质即可得出.
【解答】解:∵集合A={x|1≤x≤5},Z为整数集,
则集合A∩Z={1,2,3,4,5}.
∴集合A∩Z中元素的个数是5.
故选:B.
【点评】本题考查了集合的运算性质,考查了推理能力与计算能力,属于基础题.
3.(5分)抛物线y2=4x的焦点坐标是( )
A.(0,2)B.(0,1) C.(2,0) D.(1,0)
【考点】K8:抛物线的性质.菁优网版权所有
【专题】11:计算题;4O:定义法;5D:圆锥曲线的定义、性质与方程.
【分析】根据抛物线的标准方程及简单性质,可得答案.
【解答】解:抛物线y2=4x的焦点坐标是(1,0),
故选:D.
【点评】本题考查的知识点是抛物线的简单性质,难度不大,属于基础题.
4.(5分)为了得到函数y=sin(x+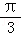 )的图象,只需把函数y=sinx的图象上所有的点( )
)的图象,只需把函数y=sinx的图象上所有的点( )
A.向左平行移动个单位长度B.向右平行移动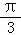 个单位长度
个单位长度
C.向上平行移动个单位长度D.向下平行移动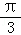 个单位长度
个单位长度
【考点】3A:函数的图象与图象的变换;HJ:函数y=Asin(ωx+φ)的图象变换.菁优网版权所有
【专题】4A:数学模型法;4O:定义法;57:三角函数的图像与性质.
【分析】根据函数图象平移“左加右减“的原则,结合平移前后函数的解析式,可得答案.
【解答】解:由已知中平移前函数解析式为y=sinx,
平移后函数解析式为:y=sin(x+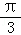 ),
),
可得平移量为向左平行移动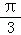 个单位长度,
个单位长度,
故选:A.
【点评】本题考查的知识点是函数图象的平移变换法则,熟练掌握图象平移“左加右减“的原则,是解答的关键.
5.(5分)设p:实数x,y满足x>1且y>1,q:实数x,y满足x+y>2,则p是q的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
【考点】29:充分条件、必要条件、充要条件.菁优网版权所有
【专题】35:转化思想;59:不等式的解法及应用;5L:简易逻辑.
【分析】由x>1且y>1,可得:x+y>2,反之不成立,例如取x=3,y=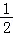 .
.
【解答】解:由x>1且y>1,可得:x+y>2,反之不成立:例如取x=3,y=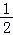 .
.
∴p是q的充分不必要条件.
故选:A.
【点评】本题考查了不等式的性质、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.
6.(5分)已知a为函数f(x)=x3﹣12x的极小值点,则a=( )
A.﹣4B.﹣2 C.4 D.2
【考点】6D:利用导数研究函数的极值.菁优网版权所有
【专题】11:计算题;33:函数思想;49:综合法;53:导数的综合应用.
【分析】可求导数得到f′(x)=3x2﹣12,可通过判断导数符号从而得出f(x)的极小值点,从而得出a的值.
【解答】解:f′(x)=3x2﹣12;
∴x<﹣2时,f′(x)>0,﹣2<x<2时,f′(x)<0,x>2时,f′(x)>0;
∴x=2是f(x)的极小值点;
又a为f(x)的极小值点;
∴a=2.
故选:D.
【点评】考查函数极小值点的定义,以及根据导数符号判断函数极值点的方法及过程,要熟悉二次函数的图象.
7.(5分)某公司为激励创新,计划逐年加大研发资金投入.若该公司2015年全年投入研发资金130万元,在此基础上,每年投入的研发资金比上一年增长12%,则该公司全年投入的研发资金开始超过200万元的年份是( )
(参考数据:lg1.12=0.05,lg1.3=0.11,lg2=0.30)
A.2018年B.2019年 C.2020年 D.2021年
【考点】88:等比数列的通项公式.菁优网版权所有
【专题】35:转化思想;54:等差数列与等比数列;59:不等式的解法及应用.
【分析】设第n年开始超过200万元,可得130×(1+12%)n﹣2015>200,两边取对数即可得出.
【解答】解:设第n年开始超过200万元,
则130×(1+12%)n﹣2015>200,
化为:(n﹣2015)lg1.12>lg2﹣lg1.3,
n﹣2015>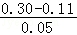 =3.8.
=3.8.
取n=2019.
因此开始超过200万元的年份是2019年.
故选:B.
【点评】本题考查了等比数列的通项公式、不等式的性质,考查了推理能力与计算能力,属于中档题.
8.(5分)秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求多项式值的一个实例,若输入n,x的值分别为3,2,则输出v的值为( )
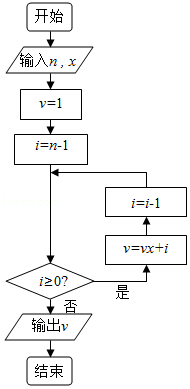
A.35B.20 C.18 D.9
【考点】EF:程序框图.菁优网版权所有
【专题】11:计算题;28:操作型;5K:算法和程序框图.
【分析】根据已知的程序框图可得,该程序的功能是利用循环结构计算并输出变量v的值,模拟程序的运行过程,可得答案.
【解答】解:∵输入的x=2,n=3,
故v=1,i=2,满足进行循环的条件,v=4,i=1,
满足进行循环的条件,v=9,i=0,
满足进行循环的条件,v=18,i=﹣1
不满足进行循环的条件,
故输出的v值为:
故选:C.
【点评】本题考查的知识点是程序框图,当循环次数不多,或有规律可循时,可采用模拟程序法进行解答.
9.(5分)已知正三角形ABC的边长为2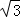 ,平面ABC内的动点P,M满足|
,平面ABC内的动点P,M满足|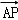 |=1,
|=1,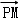 =
=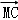 ,则|
,则|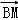 |2的最大值是( )
|2的最大值是( )
A.B.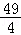 C.
C.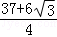 D.
D.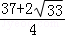
【考点】91:向量的概念与向量的模.菁优网版权所有
【专题】31:数形结合;35:转化思想;56:三角函数的求值;5A:平面向量及应用;5B:直线与圆.
【分析】如图所示,建立直角坐标系.B(0,0),C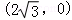 .A
.A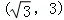 .点P的轨迹方程为:
.点P的轨迹方程为: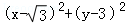 =1,令x=
=1,令x=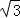 +cosθ,y=3+sinθ,θ∈[0,2π).又
+cosθ,y=3+sinθ,θ∈[0,2π).又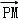 =
=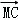 ,可得M
,可得M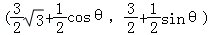 ,代入|
,代入|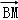 |2=
|2=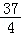 +3sin
+3sin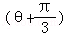 ,即可得出.
,即可得出.
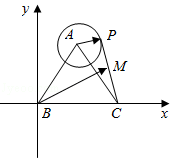
【解答】解:如图所示,建立直角坐标系.
B(0,0),C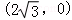 .
.
A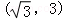 .
.
∵M满足|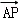 |=1,
|=1,
∴点P的轨迹方程为: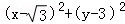 =1,
=1,
令x=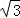 +cosθ,y=3+sinθ,θ∈[0,2π).
+cosθ,y=3+sinθ,θ∈[0,2π).
又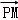 =
=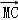 ,则M
,则M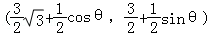 ,
,
∴|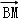 |2=
|2=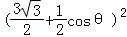 +
+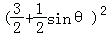 =
=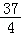 +3sin
+3sin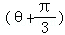 ≤
≤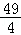 .
.
∴|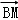 |2的最大值是
|2的最大值是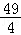 .
.
也可以以点A为坐标原点建立坐标系.
解法二:取AC中点N,MN=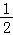 ,从而M轨迹为以N为圆心,
,从而M轨迹为以N为圆心,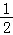 为半径的圆,B,N,M三点共线时,BM为最大值.所以BM最大值为3+
为半径的圆,B,N,M三点共线时,BM为最大值.所以BM最大值为3+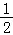 =
=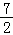 .
.
故选:B.
【点评】本题考查了数量积运算性质、圆的参数方程、三角函数求值,考查了推理能力与计算能力,属于中档题.
10.(5分)设直线l1,l2分别是函数f(x)=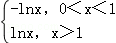 图象上点P1,P2处的切线,l1与l2垂直相交于点P,且l1,l2分别与y轴相交于点A,B,则△PAB的面积的取值范围是( )
图象上点P1,P2处的切线,l1与l2垂直相交于点P,且l1,l2分别与y轴相交于点A,B,则△PAB的面积的取值范围是( )
A.(0,1)B.(0,2) C.(0,+∞) D.(1,+∞)
【考点】6H:利用导数研究曲线上某点切线方程.菁优网版权所有
【专题】15:综合题;33:函数思想;49:综合法;53:导数的综合应用.
【分析】设出点P1,P2的坐标,求出原分段函数的导函数,得到直线l1与l2的斜率,由两直线垂直求得P1,P2的横坐标的乘积为1,再分别写出两直线的点斜式方程,求得A,B两点的纵坐标,得到|AB|,联立两直线方程求得P的横坐标,然后代入三角形面积公式,利用基本不等式求得△PAB的面积的取值范围.
【解答】解:设P1(x1,y1),P2(x2,y2)(0<x1<1<x2),
当0<x<1时,f′(x)=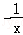 ,当x>1时,f′(x)=
,当x>1时,f′(x)=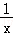 ,
,
∴l1的斜率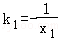 ,l2的斜率
,l2的斜率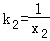 ,
,
∵l1与l2垂直,且x2>x1>0,
∴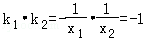 ,即x1x2=1.
,即x1x2=1.
直线l1: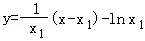 ,l2:
,l2: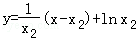 .
.
取x=0分别得到A(0,1﹣lnx1),B(0,﹣1+lnx2),
|AB|=|1﹣lnx1﹣(﹣1+lnx2)|=|2﹣(lnx1+lnx2)|=|2﹣lnx1x2|=2.
联立两直线方程可得交点P的横坐标为x=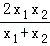 ,
,
∴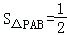 |AB|•|xP|=
|AB|•|xP|=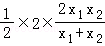 =
=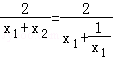 .
.
∵函数y=x+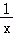 在(0,1)上为减函数,且0<x1<1,
在(0,1)上为减函数,且0<x1<1,
∴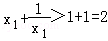 ,则
,则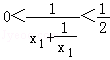 ,
,
∴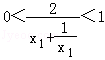 .
.
∴△PAB的面积的取值范围是(0,1).
故选:A.
【点评】本题考查利用导数研究过曲线上某点处的切线方程,训练了利用基本不等式求函数的最值,考查了数学转化思想方法,属中档题.
二、填空题:本大题共5小题,每小题5分,共25分.
11.(5分)sin750°= 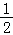 .
.
【考点】GO:运用诱导公式化简求值.菁优网版权所有
【专题】56:三角函数的求值.
【分析】利用终边相同角的诱导公式及特殊角的三角函数值即可得答案.
【解答】解:sin750°=sin(2×360°+30°)=sin30°=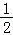 ,
,
故答案为: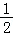 .
.
【点评】本题考查运用诱导公式化简求值,着重考查终边相同角的诱导公式及特殊角的三角函数值,属于基础题.
12.(5分)已知某三棱锥的三视图如图所示,则该三棱锥的体积是 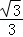 .
.
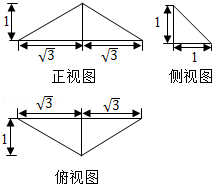
【考点】L!:由三视图求面积、体积.菁优网版权所有
【专题】11:计算题;34:方程思想;49:综合法;5F:空间位置关系与距离.
【分析】几何体为三棱锥,底面为俯视图三角形,棱锥的高为1,代入体积公式计算即可.
【解答】解:由三视图可知几何体为三棱锥,底面为俯视图三角形,底面积S=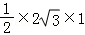 =
=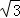 ,棱锥的高为h=1,
,棱锥的高为h=1,
∴棱锥的体积V=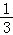 Sh=
Sh=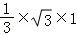 =
=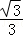 .
.
故答案为: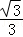 .
.
【点评】本题考查了棱锥的三视图和体积计算,是基础题.
13.(5分)从2,3,8,9中任取两个不同的数字,分别记为a,b,则logab为整数的概率是 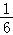 .
.
【考点】CB:古典概型及其概率计算公式.菁优网版权所有
【专题】11:计算题;35:转化思想;49:综合法;5I:概率与统计.
【分析】由已知条件先求出基本事件总数,再利用列举法求出logab为整数满足的基本事件个数,由此能求出logab为整数的概率.
【解答】解:从2,3,8,9中任取两个不同的数字,分别记为a,b,
基本事件总数n=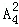 =12,
=12,
logab为整数满足的基本事件个数为(2,8),(3,9),共2个,
∴logab为整数的概率p=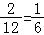 .
.
故答案为: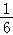 .
.
【点评】本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.
14.(5分)若函数f(x)是定义R上的周期为2的奇函数,当0<x<1时,f(x)=4x,则f(﹣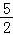 )+f(2)= ﹣2 .
)+f(2)= ﹣2 .
【考点】3K:函数奇偶性的性质与判断;3T:函数的值.菁优网版权所有
【专题】35:转化思想;4R:转化法;51:函数的性质及应用.
【分析】根据函数奇偶性和周期性的性质将条件进行转化求解即可.
【解答】解:∵函数f(x)是定义R上的周期为2的奇函数,当0<x<1时,f(x)=4x,
∴f(2)=f(0)=0,
f(﹣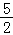 )=f(﹣
)=f(﹣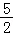 +2)=f(﹣
+2)=f(﹣ )=﹣f(
)=﹣f( )=﹣
)=﹣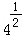 =﹣
=﹣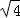 =﹣2,
=﹣2,
则f(﹣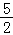 )+f(2)=﹣2+0=﹣2,
)+f(2)=﹣2+0=﹣2,
故答案为:﹣2.
【点评】本题主要考查函数值的计算,根据函数奇偶性和周期性的性质将条件进行转化是解决本题的关键.
15.(5分)在平面直角坐标系中,当P(x,y)不是原点时,定义P的“伴随点”为P′(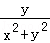 ,
,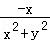 ),当P是原点时,定义“伴随点”为它自身,现有下列命题:
),当P是原点时,定义“伴随点”为它自身,现有下列命题:
①若点A的“伴随点”是点A′,则点A′的“伴随点”是点A.
②单元圆上的“伴随点”还在单位圆上.
③若两点关于x轴对称,则他们的“伴随点”关于y轴对称
④若三点在同一条直线上,则他们的“伴随点”一定共线.
其中的真命题是 ②③ .
【考点】2K:命题的真假判断与应用.菁优网版权所有
【专题】23:新定义;36:整体思想;4R:转化法;5L:简易逻辑.
【分析】根据“伴随点”的定义,分别进行判断即可,对应不成立的命题,利用特殊值法进行排除即可.
【解答】解:①设A(0,1),则A的“伴随点”为A′(1,0),
而A′(1,0)的“伴随点”为(0,﹣1),不是A,故①错误,
②若点在单位圆上,则x2+y2=1,
即P(x,y)不是原点时,定义P的“伴随点”为P(y,﹣x),
满足y2+(﹣x)2=1,即P′也在单位圆上,故②正确,
③若两点关于x轴对称,设P(x,y),对称点为Q(x,﹣y),
则Q(x,﹣y)的“伴随点”为Q′(﹣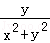 ,
,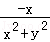 ),
),
则Q′(﹣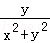 ,
,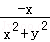 )与P′(
)与P′(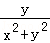 ,
,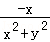 )关于y轴对称,故③正确,
)关于y轴对称,故③正确,
④∵(﹣1,1),(0,1),(1,1)三点在直线y=1上,
∴(﹣1,1)的“伴随点”为(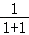 ,
,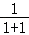 ),即(
),即(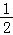 ,
,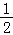 ),
),
(0,1)的“伴随点”为(1,0),(1,1的“伴随点”为(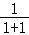 ,﹣
,﹣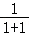 ),即(
),即(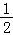 ,﹣
,﹣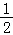 ),
),
则(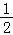 ,
,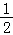 ),(1,0),(
),(1,0),(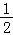 ,﹣
,﹣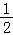 )三点不在同一直线上,故④错误,
)三点不在同一直线上,故④错误,
故答案为:②③
【点评】本题主要考查命题的真假判断,正确理解“伴随点”的定义是解决本题的关键.考查学生的推理能力.
三、解答题(共6小题,满分75分)
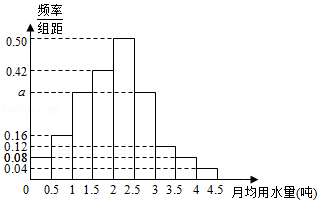
16.(12分)我国是世界上严重缺水的国家.某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨).将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(Ⅰ)求直方图中a的值;
(Ⅱ)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(Ⅲ)估计居民月均水量的中位数.
【考点】B8:频率分布直方图;BB:众数、中位数、平均数.菁优网版权所有
【专题】38:对应思想;49:综合法;5I:概率与统计.
【分析】(I)先根据频率分布直方图中的频率等于纵坐标乘以组距求出9个矩形的面积即频率,再根据直方图的总频率为1求出a的值;
(II)根据已知中的频率分布直方图先求出月均用水量不低于3吨的频率,结合样本容量为30万,进而得解.
(Ⅲ)根据频率分布直方图,求出使直方图中左右两边频率相等对应的横坐标的值.
【解答】解:(I)∵1=(0.08+0.16+a+0.40+0.52+a+0.12+0.08+0.04)×0.5,
整理可得:2=1.4+2a,
∴解得:a=0.3.
(II)估计全市居民中月均用水量不低于3吨的人数为3.6万,理由如下:
由已知中的频率分布直方图可得月均用水量不低于3吨的频率为(0.12+0.08+0.04)×0.5=0.12,
又样本容量为30万,
则样本中月均用水量不低于3吨的户数为30×0.12=3.6万.
(Ⅲ)根据频率分布直方图,得;
0.08×0.5+0.16×0.5+0.30×0.5+0.42×0.5=0.48<0.5,
0.48+0.5×0.52=0.74>0.5,
∴中位数应在(2,2.5]组内,设出未知数x,
令0.08×0.5+0.16×0.5+0.30×0.5+0.42×0.5+0.52×x=0.5,
解得x=0.04;
∴中位数是2+0.04=2.04.
【点评】本题用样本估计总体,是研究统计问题的一个基本思想方法.频率分布直方图中小长方形的面积=组距× ,各个矩形面积之和等于1,能根据直方图求众数和中位数,属于常规题型.
,各个矩形面积之和等于1,能根据直方图求众数和中位数,属于常规题型.
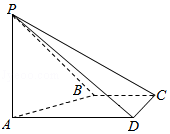
17.(12分)如图,在四棱锥P﹣ABCD中,PA⊥CD,AD∥BC,∠ADC=∠PAB=90°,BC=CD=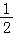 AD.
AD.
(Ⅰ)在平面PAD内找一点M,使得直线CM∥平面PAB,并说明理由;
(Ⅱ)证明:平面PAB⊥平面PBD.
【考点】LS:直线与平面平行;LY:平面与平面垂直.菁优网版权所有
【专题】14:证明题;35:转化思想;49:综合法;5F:空间位置关系与距离.
【分析】(I)M为PD的中点,直线CM∥平面PAB.取AD的中点E,连接CM,ME,CE,则ME∥PA,证明平面CME∥平面PAB,即可证明直线CM∥平面PAB;
(II)证明:BD⊥平面PAB,即可证明平面PAB⊥平面PBD.
【解答】证明:(I)M为PD的中点,直线CM∥平面PAB.
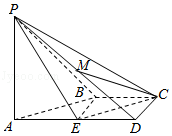
取AD的中点E,连接CM,ME,CE,则ME∥PA,
∵ME⊄平面PAB,PA⊂平面PAB,
∴ME∥平面PAB.
∵AD∥BC,BC=AE,
∴ABCE是平行四边形,
∴CE∥AB.
∵CE⊄平面PAB,AB⊂平面PAB,
∴CE∥平面PAB.
∵ME∩CE=E,
∴平面CME∥平面PAB,
∵CM⊂平面CME,
∴CM∥平面PAB
若M为AD的中点,连接CM,
由四边形ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=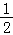 AD.
AD.
可得四边形ABCM为平行四边形,即有CM∥AB,
CM⊄平面PAB,AB⊂平面PAB,
∴CM∥平面PAB;
(II)∵PA⊥CD,∠PAB=90°,AB与CD相交,
∴PA⊥平面ABCD,
∵BD⊂平面ABCD,
∴PA⊥BD,
由(I)及BC=CD=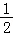 AD,可得∠BAD=∠BDA=45°,
AD,可得∠BAD=∠BDA=45°,
∴∠ABD=90°,∴BD⊥AB,
∵PA∩AB=A,
∴BD⊥平面PAB,
∵BD⊂平面PBD,
∴平面PAB⊥平面PBD.
【点评】本题主要考查了直线与平面平行的判定,平面与平面垂直的判定,考查空间想象能力、运算能力和推理论证能力,属于中档题.
18.(12分)在△ABC中,角A,B,C所对的边分别是a,b,c,且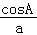 +
+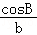 =
=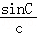 .
.
(Ⅰ)证明:sinAsinB=sinC;
(Ⅱ)若b2+c2﹣a2=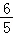 bc,求tanB.
bc,求tanB.
【考点】HP:正弦定理;HR:余弦定理.菁优网版权所有
【专题】11:计算题;29:规律型;35:转化思想;58:解三角形.
【分析】(Ⅰ)将已知等式通分后利用两角和的正弦函数公式整理,利用正弦定理,即可证明.
(Ⅱ)由余弦定理求出A的余弦函数值,利用(Ⅰ)的条件,求解B的正切函数值即可.
【解答】(Ⅰ)证明:在△ABC中,∵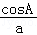 +
+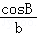 =
=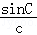 ,
,
∴由正弦定理得: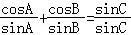 ,
,
∴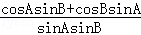 =
=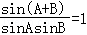 ,
,
∵sin(A+B)=sinC.
∴整理可得:sinAsinB=sinC,
(Ⅱ)解:b2+c2﹣a2=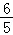 bc,由余弦定理可得cosA=
bc,由余弦定理可得cosA=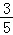 .
.
sinA=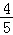 ,
,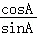 =
=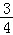
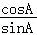 +
+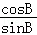 =
=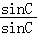 =1,
=1,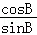 =
=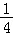 ,
,
tanB=4.
【点评】本题主要考查了正弦定理,余弦定理,两角和的正弦函数公式,三角形内角和定理,三角形面积公式的应用,考查了转化思想,属于中档题.
19.(12分)已知数列{an}的首项为1,Sn为数列{an}的前n项和,Sn+1=qSn+1,其中q>0,n∈N+
(Ⅰ)若a2,a3,a2+a3成等差数列,求数列{an}的通项公式;
(Ⅱ)设双曲线x2﹣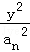 =1的离心率为en,且e2=2,求e12+e22+…+en2.
=1的离心率为en,且e2=2,求e12+e22+…+en2.
【考点】8E:数列的求和;8H:数列递推式.菁优网版权所有
【专题】11:计算题;35:转化思想;49:综合法;54:等差数列与等比数列.
【分析】(Ⅰ)根据题意,由数列的递推公式可得a2与a3的值,又由a2,a3,a2+a3成等差数列,可得2a3=a2+(a2+a3),代入a2与a3的值可得q2=2q,解可得q的值,进而可得Sn+1=2Sn+1,进而可得Sn=2Sn﹣1+1,将两式相减可得an=2an﹣1,即可得数列{an}是以1为首项,公比为2的等比数列,由等比数列的通项公式计算可得答案;
(Ⅱ)根据题意Sn+1=qSn+1,同理有Sn=qSn﹣1+1,将两式相减可得an=qan﹣1,分析可得an=qn﹣1;又由双曲线x2﹣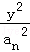 =1的离心率为en,且e2=2,分析可得e2=
=1的离心率为en,且e2=2,分析可得e2=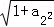 =2,
=2,
解可得a2的值,由an=qn﹣1可得q的值,进而可得数列{an}的通项公式,再次由双曲线的几何性质可得en2=1+an2=1+3n﹣1,运用分组求和法计算可得答案.
【解答】解:(Ⅰ)根据题意,数列{an}的首项为1,即a1=1,
又由Sn+1=qSn+1,则S2=qa1+1,则a2=q,
又有S3=qS2+1,则有a3=q2,
若a2,a3,a2+a3成等差数列,即2a3=a2+(a2+a3),
则可得q2=2q,(q>0),
解可得q=2,
则有Sn+1=2Sn+1,①
进而有Sn=2Sn﹣1+1,②
①﹣②可得an=2an﹣1,
则数列{an}是以1为首项,公比为2的等比数列,
则an=1×2n﹣1=2n﹣1;
(Ⅱ)根据题意,有Sn+1=qSn+1,③
同理可得Sn=qSn﹣1+1,④
③﹣④可得:an=qan﹣1,
又由q>0,
则数列{an}是以1为首项,公比为q的等比数列,则an=1×qn﹣1=qn﹣1;
若e2=2,则e2=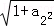 =2,
=2,
解可得a2=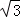 ,
,
则a2=q=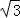 ,即q=
,即q=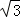 ,
,
an=1×qn﹣1=qn﹣1=(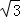 )n﹣1,
)n﹣1,
则en2=1+an2=1+3n﹣1,
故e12+e22+…+en2=n+(1+3+32+…+3n﹣1)=n+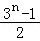 .
.
【点评】本题考查数列的递推公式以及数列的求和,涉及双曲线的简单几何性质,注意题目中q>0这一条件.
20.(13分)已知椭圆E: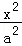 +
+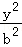 =1(a>b>0)的一个焦点与短轴的两个端点是正三角形的三个顶点,点P(
=1(a>b>0)的一个焦点与短轴的两个端点是正三角形的三个顶点,点P(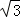 ,
,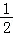 )在椭圆E上.
)在椭圆E上.
(Ⅰ)求椭圆E的方程;
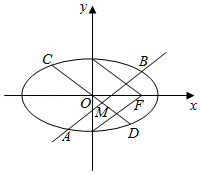
(Ⅱ)设不过原点O且斜率为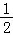 的直线l与椭圆E交于不同的两点A,B,线段AB的中点为M,直线OM与椭圆E交于C,D,证明:|MA|•|MB|=|MC|•|MD|
的直线l与椭圆E交于不同的两点A,B,线段AB的中点为M,直线OM与椭圆E交于C,D,证明:|MA|•|MB|=|MC|•|MD|
【考点】K3:椭圆的标准方程;KH:直线与圆锥曲线的综合.菁优网版权所有
【专题】15:综合题;34:方程思想;49:综合法;5D:圆锥曲线的定义、性质与方程.
【分析】(Ⅰ)由题意可得a=2b,再把已知点的坐标代入椭圆方程,结合隐含条件求得a,b得答案;
(Ⅱ)设出直线方程,与椭圆方程联立,求出弦长及AB中点坐标,得到OM所在直线方程,再与椭圆方程联立,求出C,D的坐标,把|MA|•|MB|化为(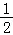 |AB|)2,再由两点间的距离公式求得|MC|•|MD|的值得答案.
|AB|)2,再由两点间的距离公式求得|MC|•|MD|的值得答案.
【解答】(Ⅰ)解:如图,
由题意可得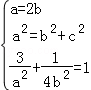 ,解得a2=4,b2=1,
,解得a2=4,b2=1,
∴椭圆E的方程为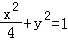 ;
;
(Ⅱ)证明:设AB所在直线方程为y=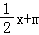 ,
,
联立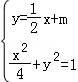 ,得x2+2mx+2m2﹣2=0.
,得x2+2mx+2m2﹣2=0.
∴△=4m2﹣4(2m2﹣2)=8﹣4m2>0,即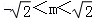 .
.
设A(x1,y1),B(x2,y2),M(x0,y0),
则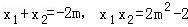 ,
,
|AB|=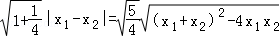 =
=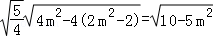 .
.
∴x0=﹣m,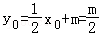 ,即M(
,即M(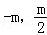 ),
),
则OM所在直线方程为y=﹣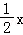 ,
,
联立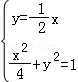 ,得
,得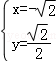 或
或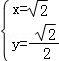 .
.
∴C(﹣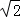 ,
,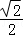 ),D(
),D(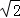 ,﹣
,﹣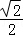 ).
).
则|MC|•|MD|=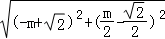
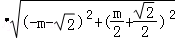
=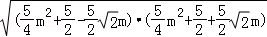 =
=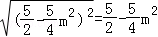 .
.
而|MA|•|MB|=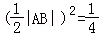 (10﹣5m2)=
(10﹣5m2)=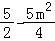 .
.
∴|MA|•|MB|=|MC|•|MD|.
【点评】本题考查椭圆的标准方程,考查了直线与圆锥曲线位置关系的应用,训练了弦长公式的应用,考查数学转化思想方法,训练了计算能力,是中档题.
21.(14分)设函数f(x)=ax2﹣a﹣lnx,g(x)=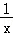 ﹣
﹣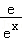 ,其中a∈R,e=2.718…为自然对数的底数.
,其中a∈R,e=2.718…为自然对数的底数.
(1)讨论f(x)的单调性;
(2)证明:当x>1时,g(x)>0;
(3)确定a的所有可能取值,使得f(x)>g(x)在区间(1,+∞)内恒成立.
【考点】3K:函数奇偶性的性质与判断;6B:利用导数研究函数的单调性;6E:利用导数研究函数的最值.菁优网版权所有
【专题】15:综合题;35:转化思想;49:综合法;53:导数的综合应用.
【分析】(Ⅰ)求导数,分类讨论,即可讨论f(x)的单调性;
(Ⅱ)要证g(x)>0(x>1),即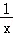 ﹣
﹣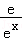 >0,即证
>0,即证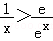 ,也就是证
,也就是证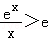 ;
;
(Ⅲ)由f(x)>g(x),得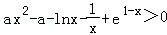 ,设t(x)=
,设t(x)=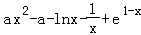 ,由题意知,t(x)>0在(1,+∞)内恒成立,再构造函数,求导数,即可确定a的取值范围.
,由题意知,t(x)>0在(1,+∞)内恒成立,再构造函数,求导数,即可确定a的取值范围.
【解答】(Ⅰ)解:由f(x)=ax2﹣a﹣lnx,得f′(x)=2ax﹣ =
=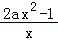 (x>0),
(x>0),
当a≤0时,f′(x)<0在(0,+∞)成立,则f(x)为(0,+∞)上的减函数;
当a>0时,由f′(x)=0,得x=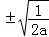 =
=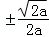 ,
,
∴当x∈(0,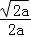 )时,f′(x)<0,当x∈(
)时,f′(x)<0,当x∈(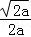 ,+∞)时,f′(x)>0,
,+∞)时,f′(x)>0,
则f(x)在(0,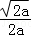 )上为减函数,在(
)上为减函数,在(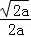 ,+∞)上为增函数;
,+∞)上为增函数;
综上,当a≤0时,f(x)为(0,+∞)上的减函数,当a>0时,f(x)在(0,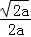 )上为减函数,在(
)上为减函数,在(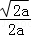 ,+∞)上为增函数;
,+∞)上为增函数;
(Ⅱ)证明:要证g(x)>0(x>1),即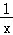 ﹣
﹣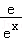 >0,
>0,
即证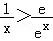 ,也就是证
,也就是证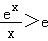 ,
,
令h(x)=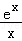 ,则h′(x)=
,则h′(x)=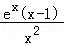 ,
,
∴h(x)在(1,+∞)上单调递增,则h(x)min=h(1)=e,
即当x>1时,h(x)>e,∴当x>1时,g(x)>0;
(Ⅲ)解:由f(x)>g(x),得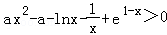 ,
,
设t(x)=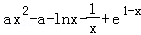 ,
,
由题意知,t(x)>0在(1,+∞)内恒成立,
∵t(1)=0,
∴有t′(x)=2ax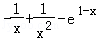 =
=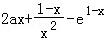 ≥0在(1,+∞)内恒成立,
≥0在(1,+∞)内恒成立,
令φ(x)=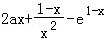 ,
,
则φ′(x)=2a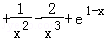 =
=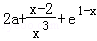 ,
,
当x≥2时,φ′(x)>0,
令h(x)=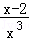 ,h′(x)=
,h′(x)=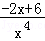 ,函数在[1,2)上单调递增,
,函数在[1,2)上单调递增,
∴h(x)min=h(1)=﹣1.
e1﹣x>0,∴1<x<2,φ′(x)>0,
综上所述,x>1,φ′(x)>0,φ(x)在区间(1,+∞)单调递增,
∴t′(x)>t′(1)≥0,即t(x)在区间(1,+∞)单调递增,
由2a﹣1≥0,
∴a≥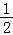 .
.
【点评】本题考查导数知识的综合运用,考查函数的单调性,不等式的证明,考查恒成立成立问题,正确构造函数,求导数是关键.

